题目内容
判断函数y=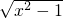 在定义域上的单调性.
在定义域上的单调性.
解:∵y=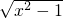 ,
,
∴该函数的定义域为(-ω,-1]∪[1,+ω)
又∵ 可看作是由
可看作是由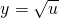 与u=x2-1两个函复合而成的.
与u=x2-1两个函复合而成的.
且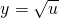 在u∈[0,+∞)上为增函数,
在u∈[0,+∞)上为增函数,
而u=x2-1∈(-∞,-1]上为减函数,
且u≥0在[1,+∞)上为增函数
当x∈(-∞,-1]时 为减函数,
为减函数,
当x≥1时, 为增函数
为增函数
分析:确定函数的定义域→判断函数y= 与u=x-1的单调性→复合函数的单调性.
与u=x-1的单调性→复合函数的单调性.
点评:本题主要考查复合函数单调性的研究方法,要转化为基本函数解决.
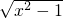 ,
,∴该函数的定义域为(-ω,-1]∪[1,+ω)
又∵
 可看作是由
可看作是由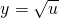 与u=x2-1两个函复合而成的.
与u=x2-1两个函复合而成的.且
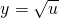 在u∈[0,+∞)上为增函数,
在u∈[0,+∞)上为增函数,而u=x2-1∈(-∞,-1]上为减函数,
且u≥0在[1,+∞)上为增函数
当x∈(-∞,-1]时
 为减函数,
为减函数,当x≥1时,
 为增函数
为增函数分析:确定函数的定义域→判断函数y=
 与u=x-1的单调性→复合函数的单调性.
与u=x-1的单调性→复合函数的单调性.点评:本题主要考查复合函数单调性的研究方法,要转化为基本函数解决.

练习册系列答案
相关题目