题目内容
已知![]() ,
,![]() ,
,![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(Ⅰ)求![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)求![]() 的解析式;
的解析式;
(III)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
解:(Ⅰ)令![]() ,得
,得![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。
。
∴![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,![]() ,
,
(Ⅱ)![]() ,
,![]() ,所以
,所以![]() 。
。
又 ![]()
∴![]() ,∴
,∴![]()
所以 ![]()
(III)当![]() 时,
时,![]() ,令
,令![]()
当![]() 时,
时,![]() 矛盾,
矛盾,
首先证明![]() 在
在![]() 恒成立.
恒成立.
令![]() ,
,![]() ,故
,故![]() 为
为![]() 上的减函数,
上的减函数,
![]() ,故
,故![]()
由(Ⅰ)可知![]() 故 当
故 当![]() 时,
时,
![]()
综上![]()


练习册系列答案
相关题目
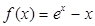 ,
,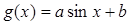 ,
,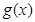 在
在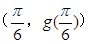 处的切线方程为
处的切线方程为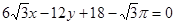
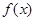 的单调区间与极值;
的单调区间与极值;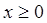 时,
时,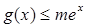 恒成立,求
恒成立,求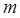 的取值范围.
的取值范围.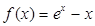 ,
,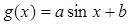 ,
, 在
在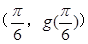 处的切线方程为
处的切线方程为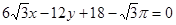
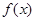 的单调区间与极值;
的单调区间与极值;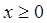 时,
时,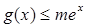 恒成立,求
恒成立,求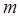 的取值范围.
的取值范围. ,
,

 ,
, 在
在 处的切线方程为
处的切线方程为 .
. 的值;
的值;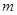 ,使得对任意的
,使得对任意的 ,总存在
,总存在 ,使得
,使得 成立?若存在,求出实数
成立?若存在,求出实数 在
在 处的切线方程为
处的切线方程为
 ,
, 在
在 时有极值,求
时有极值,求 的表达式;
的表达式; 在
在 上的值域为
上的值域为 ,求m的取值范围;
,求m的取值范围; 上单调递增,求b的取值范围.
上单调递增,求b的取值范围. 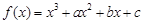 在
在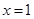 处的切线方程为
处的切线方程为
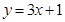 ,
,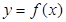 在
在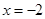 时有极值,求
时有极值,求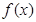 的表达式;
的表达式;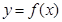 在
在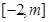 上的值域为
上的值域为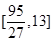 ,求m的取值范围;
,求m的取值范围;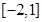 上单调递增,求b的取值范围. [
上单调递增,求b的取值范围. [