题目内容
我们规定:对于任意实数A,若存在数列{an}和实数x(x≠0),使得A=a1+a2x+a3x2+…+anxn-1,则称数A可以表示成x进制形式,简记为: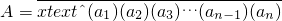 .如:
.如: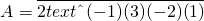 ,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.
,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.
(1)已知m=(1-2x)(1+3x2)(其中x≠0)),试将m表示成x进制的简记形式.
(2)若数列{an}满足a1=2,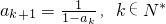 ,
,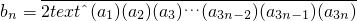 (n∈N*).求证:
(n∈N*).求证: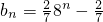 .
.
(3)若常数t满足t≠0且t>-1,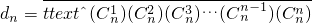 ,求
,求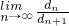 .
.
解:(1)m=(1-2x)(1+3x2)=1-2x+3x2-6x3(2分)
则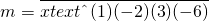 (4分)
(4分)
(2)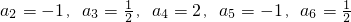 ,
,
∵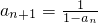 ∴
∴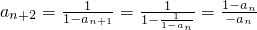
∴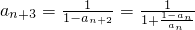 =an(n∈N*),知{an}是周期为3的数列 (6分)
=an(n∈N*),知{an}是周期为3的数列 (6分)
则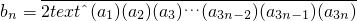
=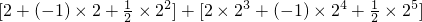
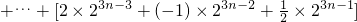 =
=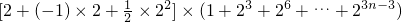 =
=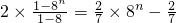 (10分)
(10分)
(3)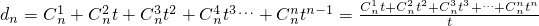 =
=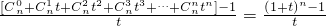 (14分)
(14分)
所以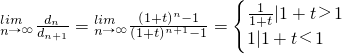 ,即
,即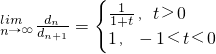 (18分)
(18分)
分析:(1)由m=(1-2x)(1+3x2)=1-2x+3x2-6x3,能将将m表示成x进制的简记形式.
(2)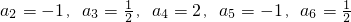 ,由
,由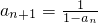 ,知
,知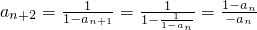 ,所以
,所以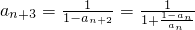 =an(n∈N*),由此能够证明
=an(n∈N*),由此能够证明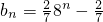 .
.
(3)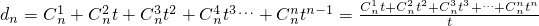 =
=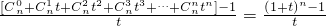 ,由此能够求出
,由此能够求出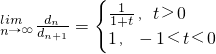 .
.
点评:本题考查数列的递推公式,解题时要认真审题,仔细解答,注意挖掘题设的隐含条件,合理地进行等价转化.
则
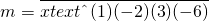 (4分)
(4分)(2)
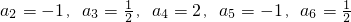 ,
,∵
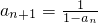 ∴
∴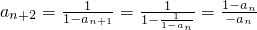
∴
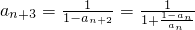 =an(n∈N*),知{an}是周期为3的数列 (6分)
=an(n∈N*),知{an}是周期为3的数列 (6分)则
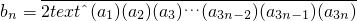
=
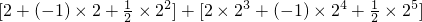
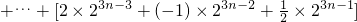 =
=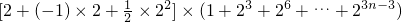 =
=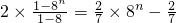 (10分)
(10分)(3)
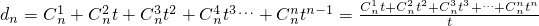 =
=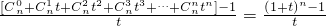 (14分)
(14分)所以
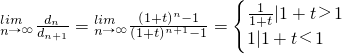 ,即
,即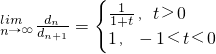 (18分)
(18分)分析:(1)由m=(1-2x)(1+3x2)=1-2x+3x2-6x3,能将将m表示成x进制的简记形式.
(2)
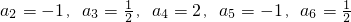 ,由
,由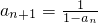 ,知
,知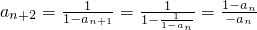 ,所以
,所以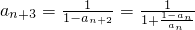 =an(n∈N*),由此能够证明
=an(n∈N*),由此能够证明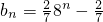 .
.(3)
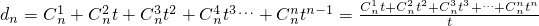 =
=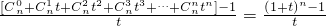 ,由此能够求出
,由此能够求出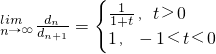 .
.点评:本题考查数列的递推公式,解题时要认真审题,仔细解答,注意挖掘题设的隐含条件,合理地进行等价转化.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 .如:
.如: ,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.
,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5. ,
, (n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由.
(n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由. ,求
,求 .
.