题目内容
等差数列 中,
中, ,
, .
.
(1)求 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
 中,
中, ,
, .
.(1)求
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前
的前 项和
项和 .
.(1) (2)
(2)
 (2)
(2)
试题分析:
(1)根据等差数列的通项公式,可知需要求出首项和公差,利用已知
 ,
, 展开联立可得首项和公差,从而得到数列的通项公式.
展开联立可得首项和公差,从而得到数列的通项公式.(2)将(1)中结果代入
 ,根据其特点,分裂该通项为
,根据其特点,分裂该通项为 ,然后求和,可以抵消除去首项和末项的所有项,从而求得数列的和.
,然后求和,可以抵消除去首项和末项的所有项,从而求得数列的和.试题解析:
(1)设等差数列
 的公差为
的公差为 d,则
d,则 .
.因为
 ,所以
,所以 .
.解得
 .
.所以
 的通项公式为
的通项公式为 .
.(2)
 .
.所以
 .
. 项和.
项和.
练习册系列答案
相关题目
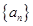 的前n项和为
的前n项和为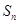 ,且满足条件
,且满足条件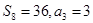
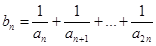 ,若对任意正整数
,若对任意正整数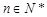 ,
,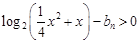 恒成立,求
恒成立,求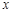 的取值范围.
的取值范围. 是首项
是首项 的递增等差数列,
的递增等差数列, 为其前
为其前 项和,且
项和,且 .
. 满足
满足 ,
, 为数列
为数列 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.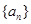 的前n项和
的前n项和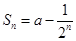 ,(1)求实数
,(1)求实数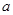 的值;(2)求数列
的值;(2)求数列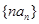 的前n项和
的前n项和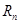 .
. 为等差数列
为等差数列 的前
的前 项和,
项和, ,
, ,则
,则 ( )
( )
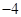


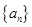 满足
满足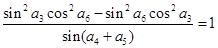 ,公差
,公差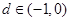 ,当且仅当
,当且仅当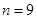 时,数列
时,数列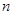 项和
项和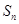 取得最大值,求该数列首项
取得最大值,求该数列首项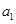 的取值范围
的取值范围



 (ab)= a
(ab)= a (n∈N*), bn=
(n∈N*), bn= (n∈N*).
(n∈N*). 的等差中项是
的等差中项是 ,且
,且 ,则
,则 的最小值是( )
的最小值是( )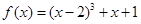 ,数列
,数列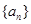 是公差不为0的等差数列,
是公差不为0的等差数列,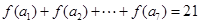 ,则
,则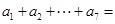 。
。