题目内容
 如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ABCD.点E、F分别为大圆上的劣弧
如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ABCD.点E、F分别为大圆上的劣弧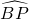 、
、 的中点,给出下列结论:
的中点,给出下列结论:
①向量 在向量
在向量 方向上的投影恰为
方向上的投影恰为 ;
;
②E、F两点的球面距离为 ;
;
③球面上到E、F两点等距离的点的轨迹是两个点;
④若点M为大圆上的劣弧 的中点,则过点M且与直线EF、PC成等角的直线只有三条,其中正确的是
的中点,则过点M且与直线EF、PC成等角的直线只有三条,其中正确的是
- A.②④
- B.①④
- C.②
- D.②③
C
分析:先建立如图所示的空间直角坐标系,写出坐标E(0, ,
, ),F(
),F( ,-
,- ,0)B(0,1,0),P(0,0,1)C(1,0,0)再一一验证即可.
,0)B(0,1,0),P(0,0,1)C(1,0,0)再一一验证即可.
解答: 解:建立如图所示的空间直角坐标系,则E(0,
解:建立如图所示的空间直角坐标系,则E(0, ,
, ),F(
),F( ,-
,- ,0)B(0,1,0),P(0,0,1)C(1,0,0)
,0)B(0,1,0),P(0,0,1)C(1,0,0)
①向量 在向量
在向量 方向上的投影为
方向上的投影为 ,错;
,错;
②cos∠EOF=cos∠EOBcos∠COB=cos45°cos(90°+45°)=- =-
=-
∴ ,对;
,对;
③过点EF的中点及球心O的大圆上任意点到点E、F的距离都相等,错;
④由于等角的值不是一定值,因此将直线EF、PC都平移到点M,可知过点M且与直线EF、PC成等角的直线有无数多条,错;
故选C.
点评:本题主要考查了球的性质、球面距离及相关计算,解答的关键是建立适当的空间坐标系写出点的坐标后利用空间坐标进行计算,属于难题.
分析:先建立如图所示的空间直角坐标系,写出坐标E(0,
 ,
, ),F(
),F( ,-
,- ,0)B(0,1,0),P(0,0,1)C(1,0,0)再一一验证即可.
,0)B(0,1,0),P(0,0,1)C(1,0,0)再一一验证即可.解答:
 解:建立如图所示的空间直角坐标系,则E(0,
解:建立如图所示的空间直角坐标系,则E(0, ,
, ),F(
),F( ,-
,- ,0)B(0,1,0),P(0,0,1)C(1,0,0)
,0)B(0,1,0),P(0,0,1)C(1,0,0)①向量
 在向量
在向量 方向上的投影为
方向上的投影为 ,错;
,错;②cos∠EOF=cos∠EOBcos∠COB=cos45°cos(90°+45°)=-
 =-
=-
∴
 ,对;
,对;③过点EF的中点及球心O的大圆上任意点到点E、F的距离都相等,错;
④由于等角的值不是一定值,因此将直线EF、PC都平移到点M,可知过点M且与直线EF、PC成等角的直线有无数多条,错;
故选C.
点评:本题主要考查了球的性质、球面距离及相关计算,解答的关键是建立适当的空间坐标系写出点的坐标后利用空间坐标进行计算,属于难题.

练习册系列答案
相关题目
 如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ACBD.点E、F分别为大圆上的劣弧
如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ACBD.点E、F分别为大圆上的劣弧
 (2011•成都二模)如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ABCD.点E、F分别为大圆上的劣弧
(2011•成都二模)如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ABCD.点E、F分别为大圆上的劣弧 中.
中. 、
、 是两条互相垂直的直径,半径
是两条互相垂直的直径,半径 平面
平面 .点
.点 、
、 分别为大圆上的劣弧
分别为大圆上的劣弧 、
、 的中点,给出下列结论:
的中点,给出下列结论: 在向量
在向量 方向上的投影恰为
方向上的投影恰为 ;
; ;
;
 为大圆上的劣弧
为大圆上的劣弧 的中点,则过点
的中点,则过点 、
、 成等角的直线只有三条,其中正确的是
成等角的直线只有三条,其中正确的是
 如图,在半径为l的球
如图,在半径为l的球