题目内容

16．求函数f（x）=$\frac{2x-1}{3x+1}$的值域．

分析 分离常数，可将原函数变成$f（x）=\frac{2}{3}-\frac{5}{3（3x+1）}$，从而根据$\frac{5}{3（3x+1）}≠0$便得出f（x）≠$\frac{2}{3}$，这样即可得出f（x）的值域．

解答 解：$f（x）=\frac{2x-1}{3x+1}=\frac{\frac{2}{3}（3x+1）-\frac{5}{3}}{3x+1}=\frac{2}{3}-\frac{5}{3（3x+1）}$；
∵$\frac{5}{3（3x+1）}≠0$；
∴$f（x）≠\frac{2}{3}$；
∴原函数的值域为：{f（x）|f（x）$≠\frac{2}{3}$}．

点评 考查函数值域的概念，分离常数法求函数值域，熟悉反比例函数的值域．

练习册系列答案
相关题目
6．已知函数f（x）=x2+ax+b，x∈[-5，5]．
（1）若函数f（x）图象过点（1，0）和（3，0）．求f（-1）的值．
（2）当a=-2，b=-5时．求函数f（x）的单调区间和值域．
（3）若函数f（x）在[-5，5]上增函数．求a的取值范围．
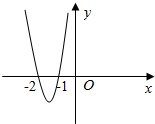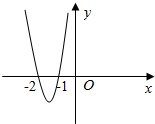7．已知函数f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，且当x＜0时，函数的部分图象如图所示，则不等式xf（x）＜0的解集是（　　）
A．{x|-2＜x＜-1，或1＜x＜2}B．{x|-2＜x＜-1，或0＜x＜1，或x＞2}
C．{x|x＜-2，或1＜x＜2}D．{x|x＜-2，或-1＜x＜0，或0＜x＜1，或x＞2}
4．在等差数列{an}中，已知a3=9，d=3，an=30，则n等于（　　）
A．7B．8C．9D．10
11．化简：（$\frac{{b}^{2}}{2{a}^{2}}$）2÷（-$\frac{4{b}^{3}}{{a}^{-7}}$）×（$\frac{{b}^{2}}{a}$）3．
1．求证：
（1）f（x）=|x+3|+|x-3|是R上的偶函数；
（2）f（x）=|x+3|-|x-3|是R上的奇函数．
8．已知f（x）是定义在R上的周期函数，最小正周期为T，则下列函数中恒为周期函数的是（　　）
A．f（x2+x）B．f（2x+x）C．f（sinx+x）D．f（f（x）+x）
5．已知${x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}}$=4，求$\frac{x+{x}^{-1}+4}{{x}^{2}+{x}^{-2}-200}$的值．
6．下列数列是等比数列的是（　　）
A．1，1，1，1，…B．…0，0，0，0，C．0，12，14，18，…D．-1，-1，1，1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网