Question

已知α、β都是锐角，且sinβ＝sinαcos(α＋β)．

(1)当α＋β＝，求tanβ的值；

(2)当tanβ取最大值时，求tan(α＋β)的值．

Answer 1

　(1)∵由条件知，sinβ＝sin，

整理得sinβ－cosβ＝0，∵β为锐角，∴tanβ＝.

(2)由已知得sinβ＝sinαcosαcosβ－sin²αsinβ，

∴tanβ＝sinαcosα－sin²αtanβ，

∴tanβ＝＝

＝＝≤＝.

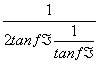当且仅当＝2tanα时，取“＝”号，

∴tanα＝时，tanβ取得最大值，

此时，tan(α＋β)＝＝.