题目内容
已知函数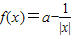 .
.(1)求证:y=f(x)在(0,+∞)上是增函数;
(2)若函数y=f(x)在[m,n]上的值域是[m,n](m≠n),求实数a的取值范围.
【答案】分析:(1)(0,+∞)时,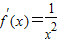 >0,y=f(x)在(0,+∞)上是增函数.由此能够证明y=f(x)在(0,+∞)上是增函数.
>0,y=f(x)在(0,+∞)上是增函数.由此能够证明y=f(x)在(0,+∞)上是增函数.
(2)函数的定义域:x>0或x<0.当x>0时,f(x)=a-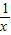 单调递增;当x<0时,f(x)=a+
单调递增;当x<0时,f(x)=a+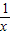 单调递减.当x>0时,f(m)=m且f(n)=n且m<n,即m=a-
单调递减.当x>0时,f(m)=m且f(n)=n且m<n,即m=a-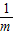 ,且n=a-
,且n=a-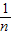 ,且m<n,这个式子等价于方程二元一次方程x2-ax+1=0有两个正的不等实根,由此能求出a的取值范围.
,且m<n,这个式子等价于方程二元一次方程x2-ax+1=0有两个正的不等实根,由此能求出a的取值范围.
解答:(1)证明:∵(0,+∞)时,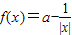 =a-
=a-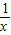 ,
,
∴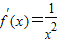 >0,
>0,
∴y=f(x)在(0,+∞)上是增函数.
(2)解:函数的定义域:x>0或x<0.
当x>0时,f(x)=a-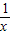 单调递增;当x<0时,f(x)=a+
单调递增;当x<0时,f(x)=a+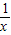 单调递减.
单调递减.
当x>0时,f(m)=m且f(n)=n且m<n,即m=a-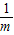 ,且n=a-
,且n=a-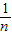 ,且m<n,
,且m<n,
这个式子等价于方程
x=a-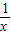 有两个不等实根,即二元一次方程x2-ax+1=0有两个正的不等实根,
有两个不等实根,即二元一次方程x2-ax+1=0有两个正的不等实根,
当x<0时,f(m)=n且f(n)=m,即a+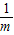 =n,且a+
=n,且a+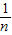 =m,且m<n<0,
=m,且m<n<0,
a=n-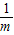 =m-
=m-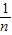 .
.
根据以上情况,有:
①对称轴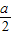 ,判别式△=a2-4>0,且x=0时等式左边=1>0.解得a>2.
,判别式△=a2-4>0,且x=0时等式左边=1>0.解得a>2.
②a2=nm+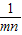 -2,
-2,
a-a=(n-m)-(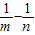 )=(n-m)-
)=(n-m)-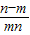 =(n-m)(1-
=(n-m)(1-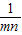 )=0,
)=0,
因为n-m≠0,所以1-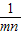 =0,即mn=1,所以a2=1+1-2=0
=0,即mn=1,所以a2=1+1-2=0
综上所述,a的取值范围是{a|a>2或a=0}.
点评:本题考查函数的单调性的证明,考查实数的取值范围的求法.解题时要认真审题,仔细解答,注意导数性质的灵活运用,合理地进行等价转化.
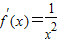 >0,y=f(x)在(0,+∞)上是增函数.由此能够证明y=f(x)在(0,+∞)上是增函数.
>0,y=f(x)在(0,+∞)上是增函数.由此能够证明y=f(x)在(0,+∞)上是增函数.(2)函数的定义域:x>0或x<0.当x>0时,f(x)=a-
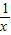 单调递增;当x<0时,f(x)=a+
单调递增;当x<0时,f(x)=a+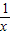 单调递减.当x>0时,f(m)=m且f(n)=n且m<n,即m=a-
单调递减.当x>0时,f(m)=m且f(n)=n且m<n,即m=a-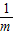 ,且n=a-
,且n=a-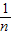 ,且m<n,这个式子等价于方程二元一次方程x2-ax+1=0有两个正的不等实根,由此能求出a的取值范围.
,且m<n,这个式子等价于方程二元一次方程x2-ax+1=0有两个正的不等实根,由此能求出a的取值范围.解答:(1)证明:∵(0,+∞)时,
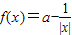 =a-
=a-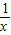 ,
,∴
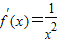 >0,
>0,∴y=f(x)在(0,+∞)上是增函数.
(2)解:函数的定义域:x>0或x<0.
当x>0时,f(x)=a-
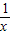 单调递增;当x<0时,f(x)=a+
单调递增;当x<0时,f(x)=a+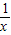 单调递减.
单调递减.当x>0时,f(m)=m且f(n)=n且m<n,即m=a-
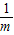 ,且n=a-
,且n=a-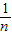 ,且m<n,
,且m<n,这个式子等价于方程
x=a-
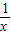 有两个不等实根,即二元一次方程x2-ax+1=0有两个正的不等实根,
有两个不等实根,即二元一次方程x2-ax+1=0有两个正的不等实根,当x<0时,f(m)=n且f(n)=m,即a+
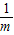 =n,且a+
=n,且a+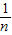 =m,且m<n<0,
=m,且m<n<0,a=n-
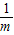 =m-
=m-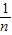 .
.根据以上情况,有:
①对称轴
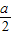 ,判别式△=a2-4>0,且x=0时等式左边=1>0.解得a>2.
,判别式△=a2-4>0,且x=0时等式左边=1>0.解得a>2.②a2=nm+
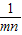 -2,
-2,a-a=(n-m)-(
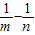 )=(n-m)-
)=(n-m)-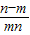 =(n-m)(1-
=(n-m)(1-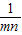 )=0,
)=0,因为n-m≠0,所以1-
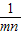 =0,即mn=1,所以a2=1+1-2=0
=0,即mn=1,所以a2=1+1-2=0综上所述,a的取值范围是{a|a>2或a=0}.
点评:本题考查函数的单调性的证明,考查实数的取值范围的求法.解题时要认真审题,仔细解答,注意导数性质的灵活运用,合理地进行等价转化.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目





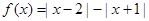 .
. ;
;
 .
. ;
; .
. .
. 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
) 时,若关于
时,若关于 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围. .
. 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
) 时,若关于
时,若关于 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.