题目内容
已知函数f(x)是在(0,+∞)上每一点处可导的函数,若xf′(x)-f(x)>0在x>0上恒成立,且f(x)=xax(a>0,a≠1,x>0),
-
=
,若数列{
}(n∈N)的前n项和为Sn,则
Sn=( )
| 7f(1) |
| 3 |
| f(2) |
| 2 |
| 2 |
| 3 |
| n |
| f(n) |
| lim |
| n→∞ |
A、
| ||
| B、1 | ||
| C、-2 | ||
D、-
|
分析:通过
-
=
,求出a 的值,利用xf′(x)-f(x)>0在x>0上恒成立,判断a的值,然后求出数列的通项公式,求
出Sn,然后求出极限即可.
| 7f(1) |
| 3 |
| f(2) |
| 2 |
| 2 |
| 3 |
出Sn,然后求出极限即可.
解答:解:f(x)=xax(a>0,a≠1,x>0),
-
=
,所以7a-3a2=2,解得a=2或a=
,
因为函数f(x)是在(0,+∞)上每一点处可导的函数,若xf′(x)-f(x)>0在x>0上恒成立,
所以(
)′>0即)ax是增函数,所以a=2,数列{
}就是{
},
所以Sn=
+
+
+…+
,因为公比为:
Sn=
=1.
故选B.
| 7f(1) |
| 3 |
| f(2) |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
因为函数f(x)是在(0,+∞)上每一点处可导的函数,若xf′(x)-f(x)>0在x>0上恒成立,
所以(
| f(x) |
| x |
| n |
| f(n) |
| 1 |
| 2n |
所以Sn=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| lim |
| n→∞ |
| ||
1-
|
故选B.
点评:本题是中档题,考查函数的导数及其应用,注意分式的导函数的应用是本题的关键,注意无穷等比数列公比小于1的数列求和的极限的应用.

练习册系列答案
相关题目
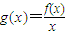 在(0,+∞)上是增函数;
在(0,+∞)上是增函数;