题目内容
已知函数f(x)是在(0,+∞)上每一点均可导的函数,若xf/(x)>f(x)在x>0时恒成立.(1)求证:函数g(x)=
| f(x) | x |
(2)求证:当x1>0,x2>0时,有f(x1+x2)>f(x1)+f(x2);
(3)请将(2)问推广到一般情况,并证明你的结论.
分析:①利用商的导数法则求g(x)=
的导数,由已知知其大于0,所以单增.
②利用①的结论及x1+x2>x2,和x1+x2>x1,证出不等式
③与正整数有关的命题用数学归纳法证
| f(x) |
| x |
②利用①的结论及x1+x2>x2,和x1+x2>x1,证出不等式
③与正整数有关的命题用数学归纳法证
解答:解:(1)由g(x)=
得g/(x)=
,因为xf/(x)>f(x),
所以g/(x)>0在x>0时恒成立,所以函数g(x)=
在(0,+∞)上是增函数.
(2)由(1)知函数g(x)=
在(0,+∞)上是增函数,所以当x1>0,x2>0时,
有
>
,
>
成立,(5分)
从而f(x1)<
f(x1+x2),f(x2)<
f(x1+x2),
两式相加得f(x1+x2)>f(x1)+f(x2).
(3)推广到一般情况为:
若xi>0(i=1,2,3n),则f(x1+x2+…+xn)>f(x1)+f(x2)+…+f(xn),n∈N,n≥2.
以下用数学归纳法证明
(1)当n=2时,有(2)已证成立,
(2)假设当n=k(k≥2)时成立,即f(x1+x2+…+xk)>f(x1)+f(x2)+…+f(xk)
那么当n=k+1时,f(x1+x2+…+xk+xk+1)>f(x1+x2+…+xk)+f(xk+1)>f(x1)+f(x2)+…+f(xk)+f(xk+1)
成立,即当n=k+1时也成立.
有(1)(2)可知不等式对一切n∈N,n≥2时都成立.(12分)
| f(x) |
| x |
| xf/(x)-f(x) |
| x2 |
所以g/(x)>0在x>0时恒成立,所以函数g(x)=
| f(x) |
| x |
(2)由(1)知函数g(x)=
| f(x) |
| x |
有
| f(x1+x2) |
| x1+x2 |
| f(x1) |
| x1 |
| f(x1+x2) |
| x1+x2 |
| f(x2) |
| x2 |
从而f(x1)<
| x1 |
| x1+x2 |
| x2 |
| x1+x2 |
两式相加得f(x1+x2)>f(x1)+f(x2).
(3)推广到一般情况为:
若xi>0(i=1,2,3n),则f(x1+x2+…+xn)>f(x1)+f(x2)+…+f(xn),n∈N,n≥2.
以下用数学归纳法证明
(1)当n=2时,有(2)已证成立,
(2)假设当n=k(k≥2)时成立,即f(x1+x2+…+xk)>f(x1)+f(x2)+…+f(xk)
那么当n=k+1时,f(x1+x2+…+xk+xk+1)>f(x1+x2+…+xk)+f(xk+1)>f(x1)+f(x2)+…+f(xk)+f(xk+1)
成立,即当n=k+1时也成立.
有(1)(2)可知不等式对一切n∈N,n≥2时都成立.(12分)
点评:本题考查导数与单调性;利用当调性及数学归纳法证不等式

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
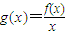 在(0,+∞)上是增函数;
在(0,+∞)上是增函数;