题目内容
3.已知f(x)=lg(ax2-2x+1).(1)若f(x)的定义域为R,求a的取值范围;
(2)如f(x)的值域为R,求a的取值范围;
(3)若f(x)在x∈[2,3]时有意义,且f(x)的最大值与最小值的差等于1,求a的值.
分析 (1)转化为ax2-2x+1>0恒成立,利用二次函数性质求解,
(2)理解函数的值域为R,则ax2-2x+1能取遍所有的正数,根二次函数性质得出a>0且△=1-4a≥0.
(3)确定a>$\frac{3}{4}$,利用f(2)=lg(4a-3),f(3)=lg(9a-5),f($\frac{1}{a}$)=lg(1-$\frac{1}{a}$),f(x)的最大值与最小值的差等于1.即可求a的值.
解答 解:(1)∵函数的定义域为R,
∴ax2-2x+1>0恒成立.
当a=0时,显然不成立.
当a≠0时,应有a>0且△=4-4a<0,
解得 a>1.
故a的取值范围为:a>1,
(2)若函数的值域为R,则ax2-2x+1能取遍所有的正数,图象不能在x轴上方
∴$\left\{\begin{array}{l}{a>0}\\{4-4a≥0}\end{array}\right.$或a=0
解得:0≤a≤1,
故a的取值范围为[0,1];
(3)在x∈[2,3]时,ax2-2x+1>0成立,∴a>-($\frac{1}{x}$-1)2+1成立,∴a>$\frac{3}{4}$,
∵f(2)=lg(4a-3),f(3)=lg(9a-5),f($\frac{1}{a}$)=lg(1-$\frac{1}{a}$),f(x)的最大值与最小值的差等于1.
∴|f(2)-f(3)|=1或|f(2)-f($\frac{1}{a}$)|=1或|f(3)-f($\frac{1}{a}$)|=1,
∴a=$\frac{\sqrt{65}-5}{4}$.
点评 本题考查了对数函数的性质,二次函数的性质,不等式的运用,属于综合题目,关键转化为不等式,理解好二次函数的性质.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
8.已知a2≤1,|b|≤1,则满足函数y=log3(x2+2ax+b)的定义域为全体实数R的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
15.已知不等式loga(1-$\frac{1}{x+2}$)>0的解集是(-∞,-2),则a的取值范围是( )
| A. | 0<a$<\frac{1}{2}$ | B. | $\frac{1}{2}$<a<1 | C. | a>2 | D. | a>1 |
17.已知函数f(x)的图象如图:则满足f(2x)•f(lg(x2-6x+120))≤0的x的取值范围是( )
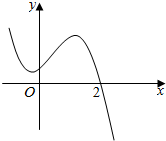

| A. | (-∞,1] | B. | [1,+∞) | C. | [0,+∞) | D. | (-∞,2] |
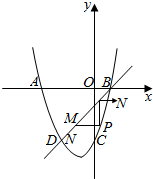 如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.
如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.