题目内容
已知函数f(x)=lnx,g(x)=k·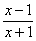 .
.
(I)求函数F(x)= f(x)- g(x)的单调区间;
(Ⅱ)当x>1时,函数f(x)> g(x)恒成立,求实数k的取值范围;
(Ⅲ)设正实数a1,a2,a3,,an满足a1+a2+a3++an=1,
求证:ln(1+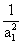 )+ln(1+
)+ln(1+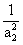 )++ln(1+
)++ln(1+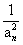 )>
)>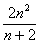 .
.
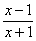 .
.(I)求函数F(x)= f(x)- g(x)的单调区间;
(Ⅱ)当x>1时,函数f(x)> g(x)恒成立,求实数k的取值范围;
(Ⅲ)设正实数a1,a2,a3,,an满足a1+a2+a3++an=1,
求证:ln(1+
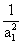 )+ln(1+
)+ln(1+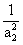 )++ln(1+
)++ln(1+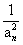 )>
)>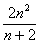 .
.(1)当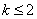 时,只有单调递增区间
时,只有单调递增区间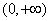
当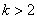 时,单调递增区间为
时,单调递增区间为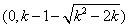 ,
,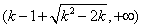
单调递减区间为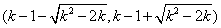
(2)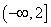
(3)由(2)知,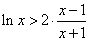 在
在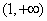 恒成立,那么构造函数借助于单调性来得到求证。
恒成立,那么构造函数借助于单调性来得到求证。
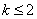 时,只有单调递增区间
时,只有单调递增区间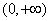
当
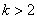 时,单调递增区间为
时,单调递增区间为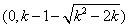 ,
,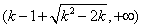
单调递减区间为
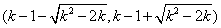
(2)
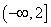
(3)由(2)知,
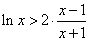 在
在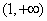 恒成立,那么构造函数借助于单调性来得到求证。
恒成立,那么构造函数借助于单调性来得到求证。试题分析:解:(Ⅰ)
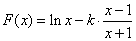
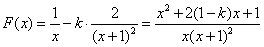 --- 1分
--- 1分由
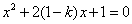 的判别式
的判别式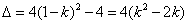
①当
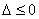 即
即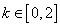 时,
时,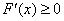 恒成立,则
恒成立,则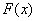 在
在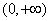 单调递增 2分
单调递增 2分②当
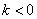 时,
时,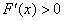 在
在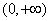 恒成立,则
恒成立,则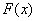 在
在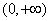 单调递增 3分
单调递增 3分③当
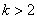 时,方程
时,方程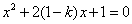 的两正根为
的两正根为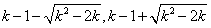
则
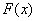 在
在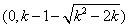 单调递增,
单调递增,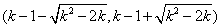 单调递减,
单调递减,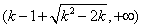 单调递增
单调递增综上,当
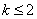 时,只有单调递增区间
时,只有单调递增区间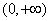
当
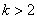 时,单调递增区间为
时,单调递增区间为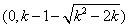 ,
,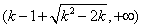
单调递减区间为
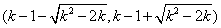 5分
5分(Ⅱ)即
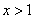 时,
时,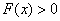 恒成立
恒成立当
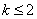 时,
时,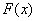 在
在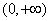 单调递增 ∴当
单调递增 ∴当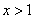 时,
时,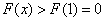 满足条件 7分
满足条件 7分当
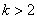 时,
时,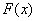 在
在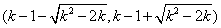 单调递减
单调递减则
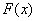 在
在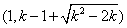 单调递减
单调递减此时
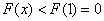 不满足条件
不满足条件故实数
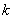 的取值范围为
的取值范围为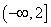 9分
9分(Ⅲ)由(2)知,
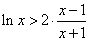 在
在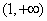 恒成立
恒成立令
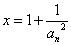 则
则 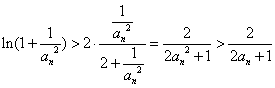 10分
10分∴
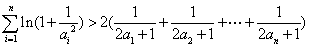 11分
11分又
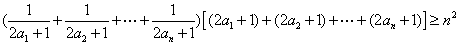
∴
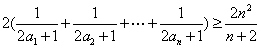 13分
13分∴
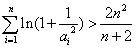
点评:主要是考查了导数在研究函数中的运用,解决的关键是利用导数的符号判定函数的单调性,进而得到不等式的证明,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
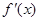 >
>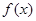 成立,则称函数
成立,则称函数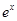 lnx是J函数时,求m的取值范围;
lnx是J函数时,求m的取值范围;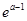 g(1)的大小;
g(1)的大小;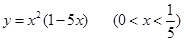 的最大值是
的最大值是 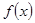 是奇函数,且在区间
是奇函数,且在区间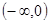 上是单调增函数,又
上是单调增函数,又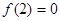 ,则
,则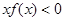 的解集为 .
的解集为 .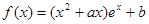 ,
,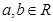 ,若函数
,若函数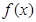 在
在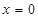 处的切线方程为
处的切线方程为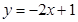 ,
,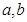 的值;
的值;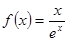 的一个单调递增区间是( )
的一个单调递增区间是( )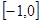

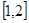
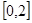
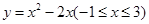 的值域是( )
的值域是( ) 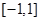

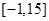
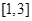
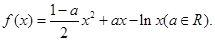
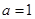 时,求函数
时,求函数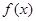 的极值;
的极值;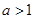 时,讨论函数
时,讨论函数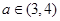 及任意
及任意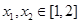 ,恒有
,恒有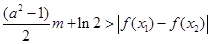 成立,求实数
成立,求实数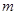 的取值范围.
的取值范围.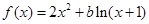 ,其中
,其中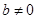 .
.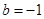 时,求在曲线
时,求在曲线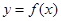 上一点
上一点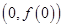 处的切线方程;
处的切线方程;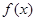 的极值点。
的极值点。