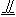题目内容
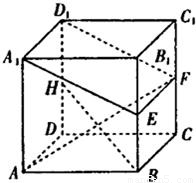
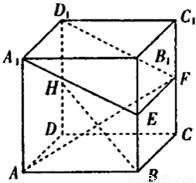
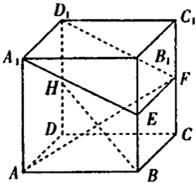 如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、H分别是棱BB1、CC1、DD1的中点.
如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、H分别是棱BB1、CC1、DD1的中点.(Ⅰ)求证:BH∥平面A1EFD1;
(Ⅱ)求直线AF与平面A1EFD1所成的角的正弦值.
分析:(Ⅰ)由已知容易证明BED1H为平行四边形,从而可得BH∥ED1,根据直线与平面平行的判定定理可证BH∥A1EFD1
(Ⅱ)过A作AG⊥A1E,垂足为G.由A1D1⊥平面A1ABB1可得A1D1⊥AG从而可证得AG⊥平面A1EFD1.则∠AFG为所求的角,从而可求AF与平面A1EFD1所成的角的正弦值
(Ⅱ)过A作AG⊥A1E,垂足为G.由A1D1⊥平面A1ABB1可得A1D1⊥AG从而可证得AG⊥平面A1EFD1.则∠AFG为所求的角,从而可求AF与平面A1EFD1所成的角的正弦值
解答:解: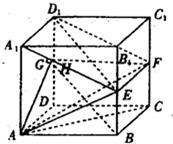 (Ⅰ)证明:连接D1E,BE=
(Ⅰ)证明:连接D1E,BE=
BB1,HD1=
DD1,BB1∥DD1,BB1=DD1
∴BE∥HD1,BE=HD1,即BED1H为平行四边形
∴BH∥ED1
∵BH?平面A1EFD1,ED1?A1EFD1
∴BH∥A1EFD1(7分)
(Ⅱ)过A作AG⊥A1E,垂足为G.
∵A1D1⊥平面A1ABB1,AG⊆A1ABB1∴A1D1⊥AG,
EA1∩A1D1=A1∴AG⊥平面A1EFD1.
连接FG,则∠AFG为所求的角.(9分)
在△AA1G中,AG•EA1=AA1•AB
∴AG=
a=
a
连接AC则AC=
a∴AF=
=
∴sin∠AFG=
=
∴F与平面A1EFD1所成的角的正弦值为
(14分)
 (Ⅰ)证明:连接D1E,BE=
(Ⅰ)证明:连接D1E,BE=| 1 |
| 2 |
| 1 |
| 2 |
∴BE∥HD1,BE=HD1,即BED1H为平行四边形
∴BH∥ED1
∵BH?平面A1EFD1,ED1?A1EFD1
∴BH∥A1EFD1(7分)
(Ⅱ)过A作AG⊥A1E,垂足为G.
∵A1D1⊥平面A1ABB1,AG⊆A1ABB1∴A1D1⊥AG,
EA1∩A1D1=A1∴AG⊥平面A1EFD1.
连接FG,则∠AFG为所求的角.(9分)
在△AA1G中,AG•EA1=AA1•AB
∴AG=
| 2 | ||
|
2
| ||
| 5 |
连接AC则AC=
| 2 |
2a2+
|
| 3a |
| 2 |
∴sin∠AFG=
| AG |
| AF |
4
| ||
| 15 |
∴F与平面A1EFD1所成的角的正弦值为
4
| ||
| 15 |
点评:直线与平面平行的判定定理是证明直线与平面平行最基本的方法,但其中的关键是要在平面内找出与已知直线平行的直线,体现了线线平行与线面平行的相互转化;而线面所成角的求解的关键是先要找出角.

练习册系列答案
相关题目