题目内容
在 中,已知
中,已知 ,则这个三角形解的情况是( )
,则这个三角形解的情况是( )
| A.有一个解 | B.有两个解 | C.无解 | D.不能确定 |
C
解析试题分析:因为, ,所以由正弦定理得,
,所以由正弦定理得, ,
, =
= >1,故这个三角形解的情况是无解,选C。
>1,故这个三角形解的情况是无解,选C。
考点:本题主要考查正弦定理的应用,正弦函数的性质。
点评:简单题,利用正弦定理判断三角形解的个数,易于出错,特别是出现如 时,要结合三角形边长取舍。
时,要结合三角形边长取舍。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
△ABC中,若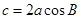 ,则△ABC的形状为( )
,则△ABC的形状为( )
| A.直角三角形 | B.等腰三角形 | C.等边三角形 | D.锐角三角形 |
△ABC中, 分别是角A,B,C所对的边,若
分别是角A,B,C所对的边,若 ,
, ,
, ,则b等于( )
,则b等于( )
A. | B. | C.2 | D.4 |
在 中,若边长和内角满足
中,若边长和内角满足 ,则角
,则角 的值是( )
的值是( )
A. | B. 或 或 | C. | D. 或 或 |
在相距 千米的
千米的 、
、 两点处测量目标
两点处测量目标 ,若
,若 ,则
,则 、
、 两点之间的距离是
两点之间的距离是
| A.4千米 | B. 千米 千米 | C. 千米 千米 | D.2千米 |
在△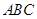 中,若
中,若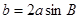 ,则
,则 等于( )
等于( )
A.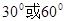 | B.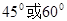 | C.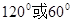 | D.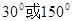 |
在 中,
中, ,则
,则 ( )
( )
A. | B. | C. | D. |
在△ABC中,A=45°,AC=4,AB= ,那么cosB=( )
,那么cosB=( )
A. | B. | C. | D. |
在△ABC中,若 ,则其面积等于( )
,则其面积等于( )
A. | B. | C. | D. |