题目内容
9.若函数y=log2(ax2+2ax+1)的定义域为R,则a的范围为[0,1).分析 由函数y=log2(ax2+2ax+1)的定义域为R,得ax2+2ax+1>0对任意实数恒成立,然后分a=0和a≠0讨论,当a≠0时,得$\left\{\begin{array}{l}{a>0}\\{4{a}^{2}-4a<0}\end{array}\right.$,求解不等式组得答案.
解答 解:∵函数y=log2(ax2+2ax+1)的定义域为R,
∴ax2+2ax+1>0对任意实数恒成立,
当a=0时,符合题意;当a≠0时,则$\left\{\begin{array}{l}{a>0}\\{4{a}^{2}-4a<0}\end{array}\right.$,解得0<a<1.
综上,使函数y=log2(ax2+2ax+1)的定义域为R的a的范围为[0,1).
故答案为:[0,1).
点评 本题考查函数的定义域及其求法,考查了数学转化思想方法,是基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
19.定义在R上的函数f(x)满足f(-x)=-f(x),f(x-2)=f(x+2),且x∈(-1,0)时,f(x)=2x,则f(log220)=( )
| A. | 1 | B. | $\frac{4}{5}$ | C. | -1 | D. | -$\frac{4}{5}$ |
20.下列语句中的赋值语句是( )
| A. | x=x^3 | B. | 2=x | C. | x=y=2 | D. | x+y=z |
17.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x^2}+{y^2}≤4\\ x-y≥0\end{array}$,则z=$\sqrt{{{(x+4)}^2}+{{(y-4)}^2}}$的最大值和最小值分别为( )
| A. | $36+16\sqrt{2}$,32 | B. | $4\sqrt{2}+2$,$4\sqrt{2}$ | C. | $36+16\sqrt{2}$,$4\sqrt{2}$ | D. | $36+16\sqrt{2}$,36 |
4.做一个容积为4升的正方形底无盖水箱,要使得材料最省,则此水箱底面边长为( )
| A. | $\frac{1}{2}$分米 | B. | 1分米 | C. | 2分米 | D. | 4分米 |
18.等比数列{an}的前n项和为Sn,S10=5,S20=20,则S30=( )
| A. | 35 | B. | 45 | C. | 65 | D. | 80 |
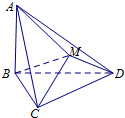 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,