题目内容
4.已知数列{an}是等差数列,满足a1+2a2=S5,下列结论中错误的是( )| A. | S9=0 | B. | S5最小 | C. | S3=S6 | D. | a5=0 |
分析 由已知条件利用等差数列的前n项和公式和通项公式求出首项和公差的关系,然后逐一核对四个选项得答案.
解答 解:∵等差数列{an}的前n项和为Sn,S5=a1+2a2,
∴$5{a}_{1}+\frac{5×4}{2}d={a}_{1}+2({a}_{1}+d)$,
解得:a1=-4d.
∴${S}_{9}=9{a}_{1}+\frac{9×8}{2}d$=0,故A正确;
${S}_{5}=5{a}_{1}+\frac{5×4}{2}d$=-10d,不一定最小,故B错误;
S3=3a1+3d=-9d,${S}_{6}=6{a}_{1}+\frac{6×5}{2}d=-9d$,故C正确;
a5=a1+4d=0,故D正确.
∴错误的结论是B.
故选:B.
点评 本题考查等差数列的通项公式,考查了等差数列的前n项和,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知集合A={x|x2-6x+5≤0},B={x|y=log2(x-2)},则A∩B=( )
| A. | (1,2) | B. | [1,2) | C. | (2,5] | D. | [2,5] |
12.已知函数f(x)=aex-2x-2a,且a∈[1,2],设函数f(x)在区间[0,ln2]上的最小值为m,则m的取值范围是( )
| A. | [-2,-2ln2] | B. | [-2,-$\frac{1}{e}$] | C. | [-2ln2,-1] | D. | [-1,-$\frac{1}{e}$] |
19.已知实数x、y满足不等式组$\left\{\begin{array}{l}y≥1\\ x-y≥0\\ x+2y-6≤0\end{array}\right.$时,目标函数z=2x+y的最大值为( )
| A. | 3 | B. | 6 | C. | 8 | D. | 9 |
9.复数z=$\frac{(i-1)^{2}+1}{{i}^{2}}$的实部为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
16.在复平面内,复数z=$\frac{3+5i}{1+i}$(i为虚数单位)对应点的坐标是( )
| A. | (1,4) | B. | (4,-1) | C. | (4,1) | D. | (-1,4) |
13.阅读材料:空间直角坐标系O-xyz中,过点P(x0,y0,z0)且一个法向量为$\overrightarrow{n}$=(a,b,c)的平面α的方程为a(x-x0)+b(y-y0)+c(z-z0)=0;过点P(x0,y0,z0)且个方向向量为$\overrightarrow{d}$=(u,v,w)(uvw≠0)的直线l的方程为$\frac{x-{x}_{0}}{u}$=$\frac{y-{y}_{0}}{v}$=$\frac{z-{z}_{0}}{w}$,阅读上面材料,并解决下面问题:已知平面α的方程为3x-5y+z-7=0,直线l是两个平面x-3y+7=0与4y+2z+1=0的交线,则直线l与平面α所成角的大小为( )
| A. | arcsin$\frac{\sqrt{10}}{35}$ | B. | arcsin$\frac{\sqrt{7}}{5}$ | C. | arcsin$\frac{\sqrt{7}}{15}$ | D. | arcsin$\frac{\sqrt{14}}{55}$ |
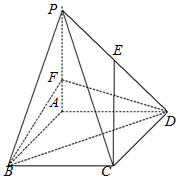 如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.
如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.