题目内容
p:?x∈R*,y=
e-
递减,q:在R上,函数y=|(
)x-1|递减.则下列命题正确的是( )
| 1 | ||
|
| x2 |
| 2 |
| 1 |
| 2 |
| A.p∨q | B.p∧q | C.?p∧q | D.q |
由题意得y=
e-
所以y′=
e-
所以函数在(0,+∞)上递减.
所以命题p是真命题.
由题意得函数y=|(
)x-1|函数在(-∞,0)上递减,在(0,+∞)上递增.
所以命题q是假命题.
由真值表p∨q是真命题.
故选A.
| 1 | ||
|
| x2 |
| 2 |
| -x | ||
|
| x2 |
| 2 |
所以命题p是真命题.
由题意得函数y=|(
| 1 |
| 2 |
所以命题q是假命题.
由真值表p∨q是真命题.
故选A.

练习册系列答案
相关题目
p:?x∈R*,y=
e-
递减,q:在R上,函数y=|(
)x-1|递减.则下列命题正确的是( )
| 1 | ||
|
| x2 |
| 2 |
| 1 |
| 2 |
| A、p∨q |
| B、p∧q |
| C、?p∧q |
| D、q |
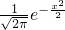 递减,q:在R上,函数y=|
递减,q:在R上,函数y=|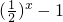 |递减.则下列命题正确的是
|递减.则下列命题正确的是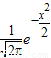 递减,q:在R上,函数y=|
递减,q:在R上,函数y=|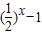 |递减.则下列命题正确的是( )
|递减.则下列命题正确的是( ) 递减,q:在R上,函数y=|
递减,q:在R上,函数y=|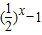 |递减.则下列命题正确的是( )
|递减.则下列命题正确的是( )