题目内容
p：?x∈R*，y=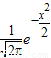
递减，q：在R上，函数y=|
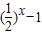|递减．则下列命题正确的是（ ）A．p∨q
B．p∧q
C．¬p∧q
D．q
【答案】分析：利用函数的性质首先判断命题p与命题q的真假性，再结合复合命题的真值表判断出复合命题的真假，进而得到正确的答案．
解答：解：由题意得y=
所以y′=
所以函数在（0，+∞）上递减．
所以命题p是真命题．
由题意得函数y=|
|函数在（-∞，0）上递减，在（0，+∞）上递增．
所以命题q是假命题．
由真值表p∨q是真命题．
故选A．
点评：解决此类问题的关键是熟悉判断简单命题与复合命题的方法，以及熟练的掌握函数的一个性质．
解答：解：由题意得y=
所以y′=所以函数在（0，+∞）上递减．所以命题p是真命题．
由题意得函数y=|
|函数在（-∞，0）上递减，在（0，+∞）上递增．所以命题q是假命题．
由真值表p∨q是真命题．
故选A．
点评：解决此类问题的关键是熟悉判断简单命题与复合命题的方法，以及熟练的掌握函数的一个性质．
练习册系列答案
名校课堂系列答案
相关题目
p：?x∈R*，y=
e-
递减，q：在R上，函数y=|(
)x-1|递减．则下列命题正确的是（ ）
| 1 | ||
|
| x2 |
| 2 |
| 1 |
| 2 |
| A、p∨q |
| B、p∧q |
| C、?p∧q |
| D、q |
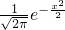递减，q：在R上，函数y=|
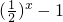|递减．则下列命题正确的是
递减，q：在R上，函数y=|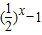
|递减．则下列命题正确的是（ ）