题目内容
15.已知抛物线Γ:x2=2py(p>0),焦点为F,点P在抛物线Γ上,且P到F的距离比P到直线y=-2的距离小1.(1)求抛物线Γ的方程;
(2)若点N为直线l:y=-5上的任意一点,过点N做抛物线Γ的切线NA与NB,切点分别为A,B,求证:直线AB恒过某一定点.
分析 (1)设P(x,y)利用条件列出方程求出p;
(2)设N(a,-5),求出切点坐标,进而求出直线AB的方程.
解答 解:(1)抛物线的准线方程为y=-$\frac{p}{2}$,
设P(x,y),则PF=y+$\frac{p}{2}$,P到直线y=-2的距离为y+2,
∴y+$\frac{p}{2}$+1=y+2,
∴p=2.
∴抛物线Γ的方程是x2=4y.
(2)抛物线方程化为f(x)=$\frac{{x}^{2}}{4}$,f′(x)=$\frac{x}{2}$.
设N(a,-5),A(x0,$\frac{{x}_{0}^{2}}{4}$),则f′(x0)=$\frac{\frac{{x}_{0}^{2}}{4}+5}{{x}_{0}-a}$,
即$\frac{{x}_{0}}{2}$=$\frac{\frac{{x}_{0}^{2}}{4}+5}{{x}_{0}-a}$,解得x0=a±$\sqrt{{a}^{2}+20}$.
∴A(a-$\sqrt{{a}^{2}+20}$,$\frac{{a}^{2}+10-a\sqrt{{a}^{2}+20}}{2}$),B(a+$\sqrt{{a}^{2}+20}$,$\frac{{a}^{2}+10+a\sqrt{{a}^{2}+20}}{2}$).
∴直线AB的方程是$\frac{y-\frac{{a}^{2}+10-a\sqrt{{a}^{2}+20}}{2}}{a\sqrt{{a}^{2}+20}}$=$\frac{x-(a-\sqrt{{a}^{2}+20})}{2\sqrt{{a}^{2}+20}}$.
整理得y=$\frac{a}{2}$x+5.
∴直线AB横过点(0,5).
点评 本题考查了抛物线的性质,曲线的切线求法,是中档题.

| A. | 42 | B. | 40$\frac{1}{2}$ | C. | 40 | D. | 21 |
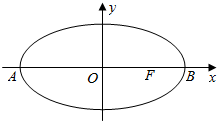 在平面直角坐标系xOy中,如图,已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
在平面直角坐标系xOy中,如图,已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.