题目内容
已知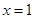 是函数
是函数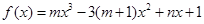 的一个极值点,其中
的一个极值点,其中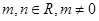
(1)求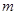 与
与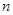 的关系式;
的关系式;
(2)求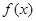 的单调区间;
的单调区间;
(3)设函数函数g(x)= 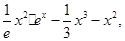
 ;试比较g(x)与
;试比较g(x)与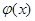 的大小。
的大小。
(1) 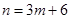
(2) 当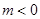 时,
时,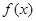 在
在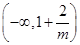 单调递减,在
单调递减,在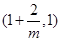 单调递增,在
单调递增,在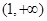 上单调递减.同理可得:当
上单调递减.同理可得:当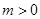 时,
时,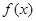 在
在 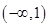 单调递增,在
单调递增,在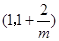 单调递减,在
单调递减,在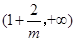 上单调递增
上单调递增
(3)  时 ,g(x)
时 ,g(x)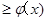
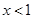 时, g(x)
时, g(x)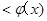
解析试题分析:解(I)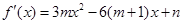 因为
因为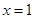 是函数
是函数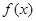 的一个极值点,所以
的一个极值点,所以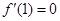 ,即
,即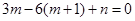 ,所以
,所以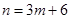 3分
3分
(II)由(I)知,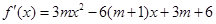 =
=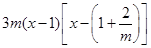 …5分
…5分
当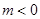 时,有
时,有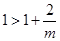 ,当
,当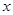 变化时,
变化时,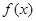 与
与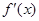 的变化如下表:
的变化如下表:
故有上表知,当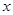
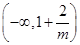
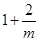
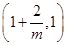
1 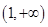
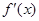
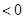
0 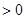
0 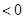
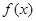
调调递减 极小值 单调递增 极大值 单调递减 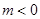 时,
时,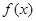 在
在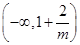

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
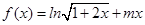 .
.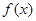 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数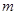 的取值范围;
的取值范围;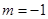 时,求函数
时,求函数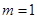 时,且
时,且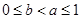 ,证明:
,证明: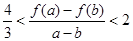 .
.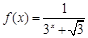 ,(1)分别求
,(1)分别求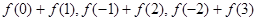 ;(2)然后归纳猜想一般性结论,并给出证明.
;(2)然后归纳猜想一般性结论,并给出证明. 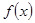 是定义在
是定义在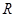 上的偶函数,且当
上的偶函数,且当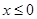 时,
时,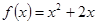 .现已画出函数
.现已画出函数 轴左侧的图像,如图所示,并根据图像
轴左侧的图像,如图所示,并根据图像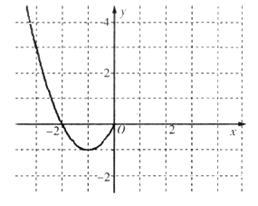
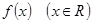 的增区间;
的增区间;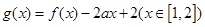 ,求函数
,求函数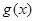 的最小值。
的最小值。
 .
.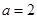 时,求
时,求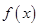 的极值;
的极值;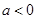 时,讨论
时,讨论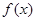 的单调性;
的单调性;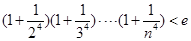 (
(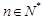 ,
,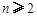 ,其中无理数
,其中无理数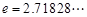 )
)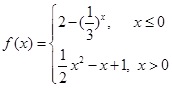 .
.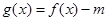 恰有3个不同零点,求实数
恰有3个不同零点,求实数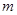 的取值范围;
的取值范围; 对所有
对所有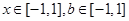 恒成立,求实数n的取值范围。
恒成立,求实数n的取值范围。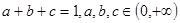 ,求证:
,求证: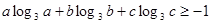 ;
;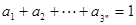 ,
,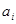 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: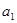
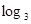
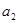
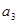
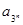
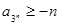
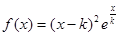 .
. 的单调区间;
的单调区间;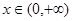 ,有
,有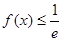 恒成立,求
恒成立,求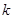 的取值范围.
的取值范围.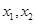 是函数
是函数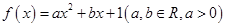 的两个零点,函数
的两个零点,函数 的最小值为
的最小值为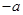 ,记
,记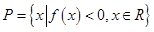
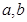 );
); 在什么范围内,函数
在什么范围内,函数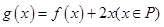 存在最小值?
存在最小值?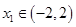 ,试确定
,试确定 的取值范围。
的取值范围。