题目内容

三棱柱OAB—O1A1B1，平面OBB1O1⊥平面OAB，∠O1OB=60°,∠AOB=90°且OB=OO1=2，OA=，求：?

(1)二面角O1-AB-O的大小；

(2)异面直线A1B与AO1所成角的大小(结果用反三角函数表示).

解析：如图，(1)取OB的中点D，连结O1D，则O1D⊥OB.?

∵平面OBB1O1⊥平面OAB,?

∴O1D⊥平面OAB.?

过D作AB的垂线，垂足为E，连结O1E，则O1E⊥AB.?

∴∠DEO1为二面角O1-AB-O的平面角.?

由题意得O1D=,sin∠OBA=,?

∴DE=DBsin∠OBA=.?

∵在Rt△O1DE中，tan∠DEO1=,?

∴∠DEO1=arctan.?

二面角O1-AB-O的大小为arctan.?

(2)以O为原点，分别以OA、OB所在直线为x、y轴，过O点且与平面AOB垂直的直线为z轴，建立空间直角坐标系，则?O(0,0,0)?,O1(0,1,),A1(,1, ),?B(0,2,0).?

设异面直线A1B与AO1所成的角为α,?

=(-,1,- ),?

=(,1,- ),?

则cosα=||=.?

∴异面直线A1B与O1A所成的角的大小为arccos.

练习册系列答案
相关题目
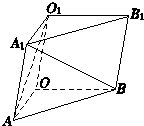如图所示，三棱柱OAB-O1A1B1中，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°，且OB=OO1=2，OA=
3
，求异面直线A1B与AO1所成角的余弦值的大小．
斜三棱柱OAB-CA1B1，其中向量
OA
=
a
，
OB
=
b
，
OC
=
.
c
，三个向量之间的夹角均为
π
3
，点M，N分别在CA1，BA1上且
CM
=
1
2
MA1
，
BN
=
NA1
，|
OA
|=2，|
OB
|=2，
|OC|
=4，如图
（1）把向量
AM
用向量
a
，
c
表示出来，并求|
AM
|；
（2）把向量
ON
用
a
，
b
，
c
表示；
（3）求AM与ON所成角的余弦值．
（2002•上海）如图，三棱柱OAB-O1A1B1，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°，且OB=OO1=2，OA=
3
，求
（1）二面角O1-AB-O的大小；
（2）异面直线A1B与AO1所成角的大小．（上述结果用反三角函数值表示）
（2009•闵行区一模）如图，直三棱柱OAB-O1A1B1中，∠AOB=90°，AA1=2，OA=
3
，OB=2，则此三棱柱的主视图的面积为
2
3
2
3
．
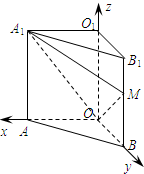（2009•闵行区一模）如图，直三棱柱OAB-O1A1B1中，∠AOB=90°，M是侧棱BB1上一点，向量
a
=(1，  1，  -1)是平面OA1M的一个法向量，则平面OAB与平面OA1M所成二面角的锐角为
arccos
3
3
arccos
3
3
（结果用反三角函数值表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网