题目内容
设△ABC的内角A,B,C所对的边长分别为a,b,c,且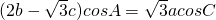 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若角 ,BC边上的中线AM的长为
,BC边上的中线AM的长为 ,求△ABC的内切圆半径r与外接圆半径R的比值.
,求△ABC的内切圆半径r与外接圆半径R的比值.
解:(Ⅰ)∵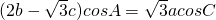 ,
,
∴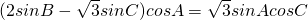 .
.
即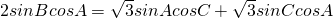 .
.
∴ .….(2分)
.….(2分)
则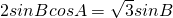 ,∴
,∴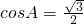 ,因为0<A<π则
,因为0<A<π则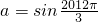 .….(4分)
.….(4分)
(Ⅱ)由(1)知 ,所以AC=BC,
,所以AC=BC,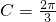 ,
,
设AC=x,在△AMC中由余弦定理得AC2+MC2-2AC•MCcosC=AM2,
即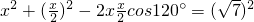 ,解得x=2,….(8分)
,解得x=2,….(8分)
故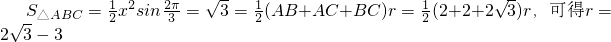 .
.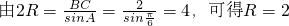 ,
,
∴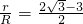 .…(12分)
.…(12分)
分析:(Ⅰ)通过已知条件利用正弦定理以及两角和与差的三角函数,化简求出角A余弦函数值,然后求出A的大小;
(Ⅱ)利用角 ,BC边上的中线AM的长为
,BC边上的中线AM的长为 ,通过余弦定理求出AC的长,通过三角形面积求出△ABC的内切圆半径r,通过正弦定理求出三角形外接圆半径R,然后求解比值.
,通过余弦定理求出AC的长,通过三角形面积求出△ABC的内切圆半径r,通过正弦定理求出三角形外接圆半径R,然后求解比值.
点评:本题考查两角和与差的三角函数,正弦定理以及余弦定理的应用,三角形的面积公式的应用,考查计算能力.
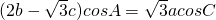 ,
,∴
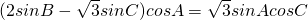 .
.即
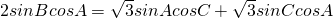 .
.∴
 .….(2分)
.….(2分)则
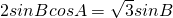 ,∴
,∴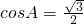 ,因为0<A<π则
,因为0<A<π则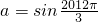 .….(4分)
.….(4分)(Ⅱ)由(1)知
 ,所以AC=BC,
,所以AC=BC,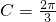 ,
,设AC=x,在△AMC中由余弦定理得AC2+MC2-2AC•MCcosC=AM2,
即
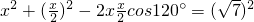 ,解得x=2,….(8分)
,解得x=2,….(8分)故
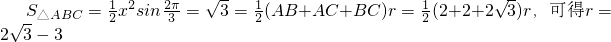 .
.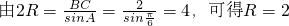 ,
,∴
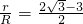 .…(12分)
.…(12分)分析:(Ⅰ)通过已知条件利用正弦定理以及两角和与差的三角函数,化简求出角A余弦函数值,然后求出A的大小;
(Ⅱ)利用角
 ,BC边上的中线AM的长为
,BC边上的中线AM的长为 ,通过余弦定理求出AC的长,通过三角形面积求出△ABC的内切圆半径r,通过正弦定理求出三角形外接圆半径R,然后求解比值.
,通过余弦定理求出AC的长,通过三角形面积求出△ABC的内切圆半径r,通过正弦定理求出三角形外接圆半径R,然后求解比值.点评:本题考查两角和与差的三角函数,正弦定理以及余弦定理的应用,三角形的面积公式的应用,考查计算能力.

练习册系列答案
相关题目