题目内容

求两曲线y=x2+1与y=3-x2在交点处的两切线的夹角.

解：解方程组得两曲线交点坐标为(1,2),(-1,2).

曲线y=x2+1在点(1,2)处的切线斜率为

k1==

=

=(2+Δx)=2.

同样,可求曲线y=3-x2在点(1,2)处的切线的斜率为k2=-2.

代入两直线的夹角公式,得两曲线在交点(1,2)处的两切线的夹角为α(0<α≤),

tanα=||=||=,所以α=arctan.

同样可求两曲线在另一交点(-1,2)处的两切线的夹角为arctan.

综上所述,两曲线在交点处夹角为arctan.

练习册系列答案
相关题目
已知定义在正实数集上的函数f（x）=x2+4ax+1，g（x）=6a2lnx+2b+1，其中a＞0．
（Ⅰ）设两曲线y=f（x），y=g（x）有公共点，且在该点处的切线相同，用a表示b，并求b的最大值；
（Ⅱ）设h（x）=f（x）+g（x），证明：若a≥
3
-1，则对任意x1，x2∈（0，+∞），x1≠x2有
h(x2)-h(x1)
x2-x1
＞8．
在平面直角坐标系xOy中，曲线y=x2-2x-3与两条坐标轴的三个交点都在圆C上．若圆C与直线x-y+a=0交于A，B两点，
（1）求圆C的方程；
（2）若|AB|=2
3
，求a的值；
（3）若 OA⊥OB，（O为原点），求a的值．
已知椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
3
2
，一个焦点坐标为F(-
3
，0)．
（1）求椭圆C1的方程；
（2）点N是椭圆的左顶点，点P是椭圆C1上不同于点N的任意一点，连接
NP并延长交椭圆右准线与点T，求
TP
NP
的取值范围；
（3）设曲线C2：y=x2-1与y轴的交点为M，过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E，（如图），记△MAB、
△MDE的面积分别是S1，S2，当
S1
S2
=
27
64
时，求直线AB的方程．
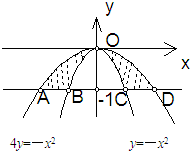如图，求由两条曲线y=-x2，4y=-x2及直线y=-1所围成图形的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网