题目内容
某学习小组进行课外研究性学习，为了测量不能到达的A、B两地，他们测得C、D两地的直线距离为2km，并用仪器测得相关角度大小如图所示，则A、B两地的距离大约等于________（提供数据：
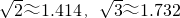，结果保留两个有效数字）
1.4km
分析：在△ADC中，可求得AC=2，在△BDC中，利用正弦定理可求得BC，最后在△ABC中，利用余弦定理可求得AB．
解答：依题意，△ADC为等边三角形，
∴AC=2；
在△BDC中，CD=2，由正弦定理得：
=
=2
，
∴BC=；
在△ABC中，由余弦定理得AB2=BC2+AC2-2BC•ACcos45°=2+4-2××2×
=2，
∴AB=≈1.4km．
故答案为：1.4km．
点评：本题考查正弦定理与余弦定理，考查解三角形，考查分析与运算能力，属于中档题．
分析：在△ADC中，可求得AC=2，在△BDC中，利用正弦定理可求得BC，最后在△ABC中，利用余弦定理可求得AB．
解答：依题意，△ADC为等边三角形，
∴AC=2；
在△BDC中，CD=2，由正弦定理得：
==2，∴BC=
；在△ABC中，由余弦定理得AB2=BC2+AC2-2BC•ACcos45°=2+4-2×
×2×=2，∴AB=
≈1.4km．故答案为：1.4km．
点评：本题考查正弦定理与余弦定理，考查解三角形，考查分析与运算能力，属于中档题．
练习册系列答案
相关题目
某中学研究性学习小组，为了考察高中学生的作文水平与爱看课外书的关系，在本校高三年级随机调查了50名学生．调査结果表明：在爱看课外书的25人中有18人作文水平好，另7人作文水平一般；在不爱看课外书的25人中有6人作文水平好，另19人作文水平一般．
（Ⅰ）试根据以上数据建立一个2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？
（Ⅱ）将其中某5名爱看课外书且作文水平好的学生分别编号为1，2，3，4，5，某5名爱看课外书且作文水平一般的学生也分别编号为1，2，3，4，5，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为3的倍数或4的倍数的概率．
附：K2=
临界值表：
（Ⅰ）试根据以上数据建立一个2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？
（Ⅱ）将其中某5名爱看课外书且作文水平好的学生分别编号为1，2，3，4，5，某5名爱看课外书且作文水平一般的学生也分别编号为1，2，3，4，5，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为3的倍数或4的倍数的概率．
附：K2=
| (a+b+c+d)(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表：
| P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某学习小组进行课外研究性学习，为了测量不能到达的A、B两地，他们测得C、D两地的直线距离2km，并用仪器测得相关角度大小如图所示，则A、B两地的距离大约等于（提供数据：
某学习小组进行课外研究性学习，为了测量不能到达的A、B两地，他们测得C、D两地的直线距离为2km，并用仪器测得相关角度大小如图所示，则A、B两地的距离大约等于
，结果保留两个有效数字）（ ）