题目内容
 某学习小组进行课外研究性学习,为了测量不能到达的A、B两地,他们测得C、D两地的直线距离2km,并用仪器测得相关角度大小如图所示,则A、B两地的距离大约等于(提供数据:
某学习小组进行课外研究性学习,为了测量不能到达的A、B两地,他们测得C、D两地的直线距离2km,并用仪器测得相关角度大小如图所示,则A、B两地的距离大约等于(提供数据:| 2 |
| 3 |
分析:依题意,在△ADC中,可求得AD=AC=CD=2km;在△BDC中,利用正弦定理可求得BC,从而在△ACB中,用余弦定理即可求得AB.
解答:解:在△ADC中,CD=2km,∠ADC=∠ACD=60°,
∴△ADC为等边三角形,
∴AD=AC=2km;
在△BDC中,∠BDC=30°,∠BCD=105°,
∴∠DBC=45°,又CD=2km,
∴由正弦定理
=
,即
=
=
得:
BC=
km.
∴在△ACB中,AC=2km,BC=
km,∠ACB=45°,
∴由余弦定理得:AB2=AC2+BC2-2×AC×BC×cos∠ACB
=4+2-2×2×
×
=2.
∴AB=
≈1.4km.
故选B.
∴△ADC为等边三角形,
∴AD=AC=2km;
在△BDC中,∠BDC=30°,∠BCD=105°,
∴∠DBC=45°,又CD=2km,
∴由正弦定理
| BC |
| sin∠BDC |
| CD |
| sin∠DBC |
| BC |
| sin30° |
| CD |
| sin45° |
| 2 |
| sin45° |
BC=
| 2 |
∴在△ACB中,AC=2km,BC=
| 2 |
∴由余弦定理得:AB2=AC2+BC2-2×AC×BC×cos∠ACB
=4+2-2×2×
| 2 |
| ||
| 2 |
=2.
∴AB=
| 2 |
故选B.
点评:本题考查解三角形的实际应用,考查正弦定理与余弦定理的综合应用,考查识图与规范解答的能力,属于中档题.

练习册系列答案
相关题目
 某学习小组进行课外研究性学习,为了测量不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小如图所示,则A、B两地的距离大约等于
某学习小组进行课外研究性学习,为了测量不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小如图所示,则A、B两地的距离大约等于 某学习小组进行课外研究性学习,为了测量不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小如图所示,则A、B两地的距离大约等于________(提供数据:
某学习小组进行课外研究性学习,为了测量不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小如图所示,则A、B两地的距离大约等于________(提供数据: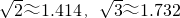 ,结果保留两个有效数字)
,结果保留两个有效数字) ,结果保留两个有效数字)( )
,结果保留两个有效数字)( )