题目内容
已知点P与定点F![]() 的距离和它到定直线l:
的距离和它到定直线l: ![]() 的距离之比是1 : 2.
的距离之比是1 : 2.
(1)求点P的轨迹C方程;
(2)过点F的直线交曲线C于A, B两点, A, B在l上的射影分别为M, N.
求证AN与BM的公共点在x轴上.
(1)![]() (2)见解析
(2)见解析
解析:
(1) 如图(1) 设P点的坐标为![]() ,
,
 则由题设得:
则由题设得: ,
,
化简得: ![]() ,
,
即![]() 即
即![]() .
.
∴点P的轨迹C的方程是![]() .
.
(2) ①当AB轴时, A、B的坐标分别为![]() ,
, ![]() ,
,
AN与BM的交点为![]() 在x轴上.
在x轴上.
②当AB不垂直于x轴时,设直线AB的方程为![]() ,
,
代入椭圆![]() ,得
,得![]()
设![]() ,
, ![]() , 则
, 则![]() ,
, ![]() ,
,
且 ∵直线AN方程是
∵直线AN方程是![]() ,
,
直线BM方程是![]() .
.
联列, 得 , 消去y, 得:
, 消去y, 得: ![]() .
.
即![]() 即
即![]() ,
,
把![]() 代入直线AN的方程
代入直线AN的方程![]()
得
 ∴AN与BM交于点
∴AN与BM交于点![]() 是x轴上一定点.
是x轴上一定点.
(2) 解法二: 如图(2) 当AB不垂直于x轴时,
设AF=n, 则AM=2n, 设BF=m, 则BN=2m,
在△ABN和△BAM中, FH∥AM, FH1∥BN,
 ∴△ABN∽△AFH和△BAM∽△BFH1
∴△ABN∽△AFH和△BAM∽△BFH1
∴![]()
![]()
![]()
同理可推, ∴![]()
![]()
![]() ,
,
∴![]() ,∴H与H1重合,∴AN与BM交点是x轴上一定点.
,∴H与H1重合,∴AN与BM交点是x轴上一定点.

练习册系列答案
相关题目
 的距离d1,是到定点F(-
的距离d1,是到定点F(- )的距离d2的
)的距离d2的 倍.
倍.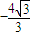 的距离d1,是到定点F(-
的距离d1,是到定点F(-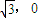 )的距离d2的
)的距离d2的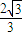 倍.
倍.