题目内容
函数 f（x）=e-xsinx的单调递增区间（k∈Z）
- A.
- B.
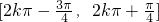
- C.
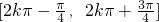
- D.
C
分析：根据利用导数研究函数的单调性的方法，先求函数的单调性，然后在R上求导数大于零的区间即可．
解答：y′=-e-xsinx+e-xcosx=e-x（cosx-sinx）＞0
∴cosx-sinx＞0，
cosx＞sinx
解得x∈，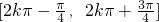
故选C．
点评：本题主要考查了利用导数研究函数的单调性，单调性是函数的重要性质，是高考的热点内容，属于基础题．
分析：根据利用导数研究函数的单调性的方法，先求函数的单调性，然后在R上求导数大于零的区间即可．
解答：y′=-e-xsinx+e-xcosx=e-x（cosx-sinx）＞0
∴cosx-sinx＞0，
cosx＞sinx
解得x∈
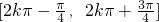，故选C．
点评：本题主要考查了利用导数研究函数的单调性，单调性是函数的重要性质，是高考的热点内容，属于基础题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
下列四个命题中，正确的是（ ）
| A、对于命题p：?x∈R，使得x2+x+1＜0，则-p：?x∈R，均有x2+x+1＞0 | ||
| B、函数f（x）=e-x-ex切线斜率的最大值是2 | ||
| C、已知ξ服从正态分布N（0，ρ2），且P（-2≤ξ≤0）=0.4，则P（ξ＞2）=0.2； | ||
D、已知函数f（a）=∫0asinxdx，则f[f（
|