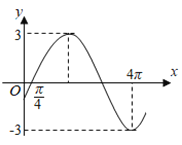
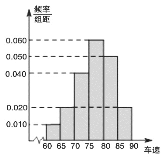
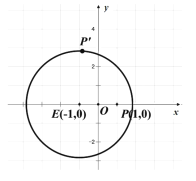
题目内容
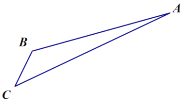
【题目】如图，游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C.现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为
.在甲出发
后，乙从A乘缆车到B，在B处停留
后，再从B匀速步行到C.假设缆车匀速直线运动的速度为
，山路AC长为
，经测量，
，
.当乙出发________分钟时，乙在缆车上与甲的距离最短.
【答案】
【解析】
在
中，根据
，
，由正弦定理求得
，得到在AB段时间
的范围，假设乙出发t分钟时，甲，乙两游客距离为d，此时，甲行走了
，乙距离A处
，由余弦定理得
，再利用二次函数求解.
在中，因为，，
所以
，
，
从而
，
.
由正弦定理得：
，得
，
所以在AB段的时间
，即
，
假设乙出发t分钟时，甲，乙两游客距离为d，此时，甲行走了，乙距离A处，
由余弦定理得
，
，
，
因为，
故
时，甲，乙两游客的距离最短.
故答案为：
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
