题目内容
直线l：y=x+b与抛物线C：x2=4y相切于点A．求实数b的值，及点A的坐标．
分析：把直线l：y=x+b与抛物线C：x2=4y的方程联立，因为直线与抛物线相切，转化为一元二次方程的判别式△=0即可得出．
解答：解：联立
．化为x2-4x-4b=0．（*）
∵直线l与抛物线C相切，∴△=（-4）2-4×（-4b）=0，解得b=-1；
代入方程（*）即为x2-4x+4=0，解得x=2，y=1，
故点A（2，1）．
|
∵直线l与抛物线C相切，∴△=（-4）2-4×（-4b）=0，解得b=-1；
代入方程（*）即为x2-4x+4=0，解得x=2，y=1，
故点A（2，1）．
点评：本题考查了直线与抛物线相切转化为方法联立利用△=0解决问题，属于基础题．
练习册系列答案
相关题目
如图，直线l：y=x+b与抛物线C：x2=4y相切于点A．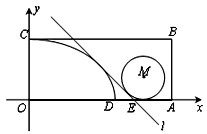
在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在x轴和y轴上（如图），且OC=1，OA=a+1（a＞1），点D在边OA上，满足OD=a．分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD．直线l：y=-x+b与椭圆弧相切，与OA交于点E．