题目内容
14. 设函数$f(x)=cos(ωx+φ)(ω>0,-\frac{π}{2}<φ<0)$的最小正周期为π,且$f(\frac{π}{4})=\frac{{\sqrt{3}}}{2}$.
设函数$f(x)=cos(ωx+φ)(ω>0,-\frac{π}{2}<φ<0)$的最小正周期为π,且$f(\frac{π}{4})=\frac{{\sqrt{3}}}{2}$.(1)求ω和φ的值;
(2)给定坐标系中作出函数f(x)在[0,π]上的图象,并结合图象写出函数的单调递减区间(直接写出结果即可,不需要叙述过程);
(3)若$f(x)>\frac{{\sqrt{2}}}{2}$,求x的取值范围.
分析 (1)根据函数的周期和条件,建立方程关系进行求解即可.
(2)利用三角函数的图象关系进行作图即可.
(3)结合三角函数的不等式进行求解.
解答 解:(1)∵函数的最小正周期为π,
∴T=$\frac{2π}{ω}$=π,则ω=2,
则f(x)=cos(2x+φ),
由$f(\frac{π}{4})=\frac{{\sqrt{3}}}{2}$得
$cos(2x+φ)=cos(2×\frac{π}{4}+φ)=cos(\frac{π}{2}+φ)=-sinφ=\frac{{\sqrt{3}}}{2}$,(4分)
即$sinφ=-\frac{{\sqrt{3}}}{2},φ=-\frac{π}{3}$.(6分)
(2)f(x)=cos(2x-$\frac{π}{3}$),
如下图(10分) 
函数的单调递减区间$[kπ+\frac{π}{6},kπ+\frac{2π}{3}],(k∈Z)$.(12分)
(3)由(1)知$f(x)=cos(2x-\frac{π}{3})$,
令$cos(2x-\frac{π}{3})>\frac{{\sqrt{2}}}{2}$,
得$2kπ-\frac{π}{4}<2x-\frac{π}{3}<2kπ+\frac{π}{4},(k∈Z)$,即$2kπ+\frac{π}{12}<2x<2kπ+\frac{7π}{12}(k∈Z)$,(14分)
得$kπ+\frac{π}{24}<x<kπ+\frac{7π}{24}(k∈Z)$,即$x∈(kπ+\frac{π}{24},kπ+\frac{7π}{24}),(k∈Z)$.(16分)
点评 本题主要考查三角函数的图象和性质,根据三角函数的图象求出ω 和φ的值是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.设α,β是两个不同的平面,m,n,l 是三条不同的直线,下列命题中正确的是( )
| A. | 若α∩β=l,m?α,n?β,则m,n一定相交 | B. | 若α∥β,m?α,n?β,则m,n一定平行 | ||
| C. | 若α∥β,m∥α,n∥β,则m,n一定平行 | D. | 若α⊥β,m⊥α,n⊥β,则m,n一定垂直 |
19.若等比数列{an}的前n项和Sn=3n-1,则其公比为( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
3.“x=-3”是“x2+3x=0”的( )
| A. | 充分必要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
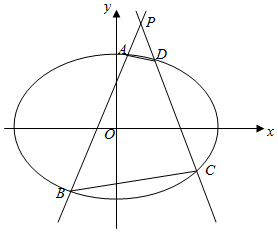 如图,在平面直角坐标系xOy中,已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),且椭圆Γ的上顶点到直线$\sqrt{3}$x+y+1=0的距离等于1.
如图,在平面直角坐标系xOy中,已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),且椭圆Γ的上顶点到直线$\sqrt{3}$x+y+1=0的距离等于1.