题目内容
已知 是非空集合,命题甲:
是非空集合,命题甲: ,命题乙:
,命题乙: ,那么 ( )
,那么 ( )
| A.甲是乙的充要条件 | B.甲是乙的充分不必要条件 |
| C.甲是乙的既不充分也不必要条件 | D.甲是乙的必要不充分条件 |
D
解析试题分析:由 可以得出
可以得出 或
或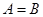 ,反之,由
,反之,由 可以得出
可以得出 ,所以甲是乙的必要不充分条件.
,所以甲是乙的必要不充分条件.
考点:本小题主要考查集合的关系和充分、必要条件的判断,考查学生的推理能力.
点评:考查集合的关系可以借助韦恩图.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
命题“ ”的否命题是 ( )
”的否命题是 ( )
A. | B.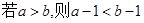 |
C. | D. |
已知命题 ,则 ( )
,则 ( )
A. | B. |
C.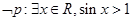 | D.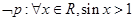 |
设p、q是两上命题, ( )
( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若命题 ;命题
;命题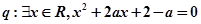
若命题“ ”是真命题,则实数
”是真命题,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
“m=4”是“直线(m+2)x+2my-1=0与直线(m+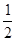 )x+(m+2)y+3=0相互平行”的
)x+(m+2)y+3=0相互平行”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要 |
下列全称命题中假命题的个数是()
①2x+1是整数(x∈R)②对所有的x∈R ,x>3③对任意一个x∈z,2x2+1为奇数
| A.0 | B.1 | C.2 | D.3 |
命题“存在一个无理数,它的平方是有理数”的否定是( )
| A.任意一个无理数,它的平方是有理数 |
| B.任意一个无理数,它的平方不是有理数 |
| C.存在一个有理数,它的平方是有理数 |
| D.存在一个有理数,它的平方不是有理数 |
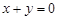 ,则
,则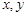 互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若
互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若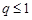 ,则
,则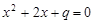 有实根”的逆命题;④“不等边三角形的三个内角相等”的逆否命题;其中真命题有( )
有实根”的逆命题;④“不等边三角形的三个内角相等”的逆否命题;其中真命题有( )