题目内容
设点P是抛物线C:x2=2py(p>0)在第一象限内的任意一点,过P作抛物线C的切线l交x轴于点M,F为抛物线C的焦点,点Q满足
=
+
,若△PFQ是面积为
的等边三角形,则p的值为
| PM |
| 1 |
| 2 |
| PF |
| 1 |
| 2 |
| PQ |
| 3 |
1
1
.分析:由抛物线方程求出焦点坐标,设出动点P的坐标,利用导数求出过点P的切线的斜率,由点斜式写出切线方程,取y=0得到点M的坐标,根据给出的向量式得到M为FQ的中点,由中点坐标公式得到Q点的坐标,再由△PFQ是面积为
的等边三角形列式计算p的值.
| 3 |
解答:解:因为抛物线C:x2=2py,所以焦点F(0,
);
设P点坐标为P(n,
),
由x2=2py,得y=
,
则y′|x=n=
.
直线PM方程为:y-
=
(x-n),取y=0得与x轴交点M(
,0);
由
=
+
,则M为FQ连线的中点.
由中点坐标公式可得Q(n,-
);
因为△PFQ是等边三角形,故有PQ2=PF2=FQ2.
由于S△PFQ=
•
=
PF2=
,∴PF=PQ=FQ=2.
PQ2=(
+
)2=
=4,所以n2+p2=4p.
FQ2=n2+p2=22=4,与上式对比可知,p=1.
故答案为1.
| p |
| 2 |
设P点坐标为P(n,
| n2 |
| 2p |
由x2=2py,得y=
| x2 |
| 2p |
则y′|x=n=
| n |
| p |
直线PM方程为:y-
| n2 |
| 2p |
| p |
| n |
| n |
| 2 |
由
| PM |
| 1 |
| 2 |
| PF |
| 1 |
| 2 |
| PQ |
由中点坐标公式可得Q(n,-
| p |
| 2 |
因为△PFQ是等边三角形,故有PQ2=PF2=FQ2.
由于S△PFQ=
| ||
| 2 |
| PF2 |
| 2 |
| ||
| 4 |
| 3 |
PQ2=(
| n2 |
| 2p |
| p |
| 2 |
| (n2+p2)2 |
| 2p2 |
FQ2=n2+p2=22=4,与上式对比可知,p=1.
故答案为1.
点评:本题考查了直线与圆锥曲线的关系,利用导数求过抛物线上点P的切线方程是解答该题的关键,考查了学生的计算能力.是中档题.

练习册系列答案
相关题目
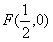 。
。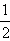 )与抛物线C交于A,B两点,且|FA|=2|FB|,求k的值;
)与抛物线C交于A,B两点,且|FA|=2|FB|,求k的值; ,若△PFQ是面积为
,若△PFQ是面积为 的等边三角形,则p的值为 .
的等边三角形,则p的值为 . .(1)求抛物线C的方程; (2)已知直线
.(1)求抛物线C的方程; (2)已知直线 与抛物线C交于A、B 两点,且|FA|=2|FB|,求k 的值; (3)设点P 是抛物线C上的动点,点R、N 在y 轴上,圆(x-1)2+y2=1 内切于△PRN,求△PRN 的面积最小值.
与抛物线C交于A、B 两点,且|FA|=2|FB|,求k 的值; (3)设点P 是抛物线C上的动点,点R、N 在y 轴上,圆(x-1)2+y2=1 内切于△PRN,求△PRN 的面积最小值.