题目内容
将函数f(x)=3sin(-2x+ )+1的图象向左平移
)+1的图象向左平移 单位,再向下平移
单位,再向下平移 单位,得到函数y=g(x)的图象.
单位,得到函数y=g(x)的图象.(1)写出y=g(x)的解析式;
(2)写出y=g(x)单调区间;
(3)写出y=g(x)的对称轴方程和对称中心的坐标.
【答案】分析:(1)根据函数y=Asin(ωx+φ)的图象变换规律可得 g(x)的解析式.
(2)令2kπ-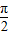 ≤2x+
≤2x+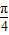 ≤2kπ+
≤2kπ+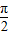 ,k∈z,求得x的范围,可得函数减区间;令2kπ+
,k∈z,求得x的范围,可得函数减区间;令2kπ+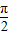 ≤2x+
≤2x+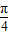 ≤2kπ+
≤2kπ+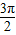 ,k∈z,求得x的范围,可得函数增区间.
,k∈z,求得x的范围,可得函数增区间.
(3)令2x+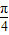 =kπ+
=kπ+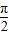 ,可得x=
,可得x=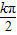 +
+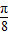 ,从而得到对称轴方程.令2x+
,从而得到对称轴方程.令2x+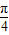 =kπ,可得x=
=kπ,可得x=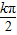 -
-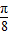 ,可得对称中心的坐标.
,可得对称中心的坐标.
解答:解:(1)根据函数y=Asin(ωx+φ)的图象变换规律可得 g(x)=-3sin(2x+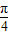 )+
)+ .…(4分)
.…(4分)
(2)令2kπ-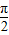 ≤2x+
≤2x+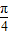 ≤2kπ+
≤2kπ+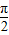 ,k∈z,求得kπ-
,k∈z,求得kπ-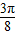 ≤x≤kπ+
≤x≤kπ+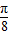 ,可得函数减区间为[kπ-
,可得函数减区间为[kπ- ,kπ+
,kπ+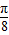 ](k∈z).
](k∈z).
令2kπ+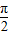 ≤2x+
≤2x+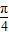 ≤2kπ+
≤2kπ+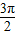 ,k∈z,求得kπ+
,k∈z,求得kπ+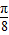 ≤x≤kπ+
≤x≤kπ+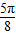 ,可得函数增区间为[kπ+
,可得函数增区间为[kπ+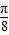 ,kπ+
,kπ+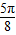 ],k∈z…(8分)
],k∈z…(8分)
(3)令2x+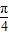 =kπ+
=kπ+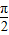 ,可得x=
,可得x=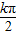 +
+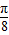 ,故对称轴方程:x=
,故对称轴方程:x= +
+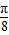 (k∈z).
(k∈z).
令2x+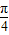 =kπ,可得x=
=kπ,可得x=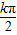 -
-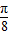 ,故对称中心:(
,故对称中心:(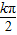 -
-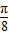 ,
, ),(k∈z)…(12分)
),(k∈z)…(12分)
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,体现了转化的数学思想,属于中档题.
(2)令2kπ-
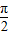 ≤2x+
≤2x+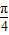 ≤2kπ+
≤2kπ+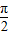 ,k∈z,求得x的范围,可得函数减区间;令2kπ+
,k∈z,求得x的范围,可得函数减区间;令2kπ+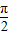 ≤2x+
≤2x+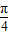 ≤2kπ+
≤2kπ+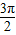 ,k∈z,求得x的范围,可得函数增区间.
,k∈z,求得x的范围,可得函数增区间.(3)令2x+
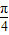 =kπ+
=kπ+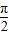 ,可得x=
,可得x=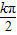 +
+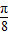 ,从而得到对称轴方程.令2x+
,从而得到对称轴方程.令2x+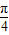 =kπ,可得x=
=kπ,可得x=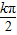 -
-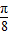 ,可得对称中心的坐标.
,可得对称中心的坐标.解答:解:(1)根据函数y=Asin(ωx+φ)的图象变换规律可得 g(x)=-3sin(2x+
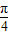 )+
)+ .…(4分)
.…(4分)(2)令2kπ-
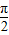 ≤2x+
≤2x+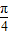 ≤2kπ+
≤2kπ+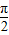 ,k∈z,求得kπ-
,k∈z,求得kπ-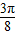 ≤x≤kπ+
≤x≤kπ+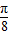 ,可得函数减区间为[kπ-
,可得函数减区间为[kπ- ,kπ+
,kπ+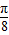 ](k∈z).
](k∈z).令2kπ+
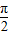 ≤2x+
≤2x+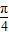 ≤2kπ+
≤2kπ+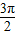 ,k∈z,求得kπ+
,k∈z,求得kπ+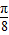 ≤x≤kπ+
≤x≤kπ+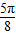 ,可得函数增区间为[kπ+
,可得函数增区间为[kπ+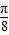 ,kπ+
,kπ+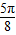 ],k∈z…(8分)
],k∈z…(8分)(3)令2x+
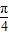 =kπ+
=kπ+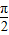 ,可得x=
,可得x=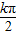 +
+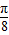 ,故对称轴方程:x=
,故对称轴方程:x= +
+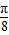 (k∈z).
(k∈z).令2x+
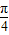 =kπ,可得x=
=kπ,可得x=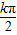 -
-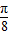 ,故对称中心:(
,故对称中心:(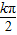 -
-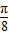 ,
, ),(k∈z)…(12分)
),(k∈z)…(12分)点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
 )图象上所有点的横坐标伸长到原来的2倍,再向右平移
)图象上所有点的横坐标伸长到原来的2倍,再向右平移 个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )



 )图象上所有点的横坐标伸长到原来的2倍,再向右平移
)图象上所有点的横坐标伸长到原来的2倍,再向右平移 个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )


