题目内容
由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y="f" -1(x)能确定数列{bn},bn=" f" –1(n),若对于任意nÎN*,都有bn=an,则称数列{bn}是数列{an}的“自反数列”.
(1)若函数f(x)=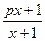 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;
(2)已知正数数列{cn}的前n项之和Sn=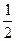 (cn+
(cn+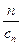 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d1=2,当n≥2时,设dn=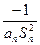 ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
(1)若函数f(x)=
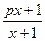 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;(2)已知正数数列{cn}的前n项之和Sn=
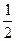 (cn+
(cn+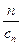 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;(3)在(1)和(2)的条件下,d1=2,当n≥2时,设dn=
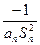 ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.(1)an=
(2)Sn= ,证明略
,证明略
(3)0<a< –1
–1

(2)Sn=
 ,证明略
,证明略(3)0<a<
 –1
–1解:(1)由题意的:f -1(x)= = f(x)=
= f(x)=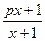 ,所以p =-1,…………2分
,所以p =-1,…………2分
所以an= ……………………………………………………………………3分翰林汇
……………………………………………………………………3分翰林汇
(2)因为正数数列{cn}的前n项之和Sn=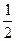 (cn+
(cn+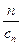 ),
),
所以c1=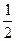 (c1+
(c1+ ),解之得:c1=1,S1=1……………………………………4分
),解之得:c1=1,S1=1……………………………………4分
当n ≥ 2时,cn = Sn–Sn–1,所以2Sn = Sn–Sn–1 + ,……………………5分
,……………………5分
Sn +Sn–1 = ,即:
,即: = n,……………………………………7分
= n,……………………………………7分
所以, = n–1,
= n–1, = n–2,……,
= n–2,……, =2,累加得:
=2,累加得:
 =2+3+4+……+ n,………………………………………………9分
=2+3+4+……+ n,………………………………………………9分
 =1+2+3+4+……+ n =
=1+2+3+4+……+ n = ,
,
Sn= ………………………………………………………………10分
………………………………………………………………10分
(3)在(1)和(2)的条件下,d1=2,
当n≥2时,设dn=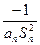 =
= =2(
=2( ),…………………13分
),…………………13分
由Dn是{dn}的前n项之和,
Dn=d1+d2+……+dn=2[1+( )+(
)+( )+(
)+( )+……+(
)+……+( )]
)]
=2(2– )………………………………………………………………………………16分
)………………………………………………………………………………16分
因为Dn>log a (1–2a)恒成立,即log a (1–2a)恒小于Dn的最小值,
显然Dn的最小值是在n=1时取得,即(Dn)min=2,
所以log a (1–2a)<2,1–2a>0,所以0<a< –1…………………………………18分
–1…………………………………18分
 = f(x)=
= f(x)=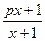 ,所以p =-1,…………2分
,所以p =-1,…………2分所以an=
 ……………………………………………………………………3分翰林汇
……………………………………………………………………3分翰林汇(2)因为正数数列{cn}的前n项之和Sn=
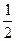 (cn+
(cn+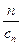 ),
),所以c1=
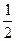 (c1+
(c1+ ),解之得:c1=1,S1=1……………………………………4分
),解之得:c1=1,S1=1……………………………………4分当n ≥ 2时,cn = Sn–Sn–1,所以2Sn = Sn–Sn–1 +
 ,……………………5分
,……………………5分Sn +Sn–1 =
 ,即:
,即: = n,……………………………………7分
= n,……………………………………7分所以,
 = n–1,
= n–1, = n–2,……,
= n–2,……, =2,累加得:
=2,累加得: =2+3+4+……+ n,………………………………………………9分
=2+3+4+……+ n,………………………………………………9分 =1+2+3+4+……+ n =
=1+2+3+4+……+ n = ,
,Sn=
 ………………………………………………………………10分
………………………………………………………………10分(3)在(1)和(2)的条件下,d1=2,
当n≥2时,设dn=
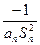 =
= =2(
=2( ),…………………13分
),…………………13分由Dn是{dn}的前n项之和,
Dn=d1+d2+……+dn=2[1+(
 )+(
)+( )+(
)+( )+……+(
)+……+( )]
)]=2(2–
 )………………………………………………………………………………16分
)………………………………………………………………………………16分因为Dn>log a (1–2a)恒成立,即log a (1–2a)恒小于Dn的最小值,
显然Dn的最小值是在n=1时取得,即(Dn)min=2,
所以log a (1–2a)<2,1–2a>0,所以0<a<
 –1…………………………………18分
–1…………………………………18分
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 中,
中, ,
,
 是否为等比数列?并说明理由;
是否为等比数列?并说明理由;
 中,已知
中,已知 ,
, ,
,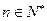 .
. 为等比数列,并求数列
为等比数列,并求数列 ,
, }、{
}、{ }的前n项和分别为
}的前n项和分别为 ,
, ,且
,且 =1(n∈N*)。
=1(n∈N*)。 ,且
,且 (n∈N*),求证:
(n∈N*),求证:
 ,
, ,
, 的第
的第 项是
项是



 ”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作
”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作 ,
, ,其中
,其中 为数列
为数列 中的第
中的第 项.
项. ,则
,则 = ; ②若
= ; ②若
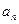 }的通项公式是
}的通项公式是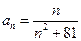 则数列{
则数列{