题目内容
(本小题满分14分)
数列{ }、{
}、{ }的前n项和分别为
}的前n项和分别为 ,
, ,且
,且 =1(n∈N*)。
=1(n∈N*)。
(1)证明数列{ }是等比数列;
}是等比数列;
(2)若数列{ }满足:
}满足: ,且
,且 (n∈N*),求证:
(n∈N*),求证:
数列{
 }、{
}、{ }的前n项和分别为
}的前n项和分别为 ,
, ,且
,且 =1(n∈N*)。
=1(n∈N*)。(1)证明数列{
 }是等比数列;
}是等比数列;(2)若数列{
 }满足:
}满足: ,且
,且 (n∈N*),求证:
(n∈N*),求证:
略
解:(1)∵ =1(n∈N*) ∴
=1(n∈N*) ∴ =1
=1
两式相减: ∴
∴ ………………3分
………………3分
∴{ }是公比为
}是公比为 的等比数列 …………………6分
的等比数列 …………………6分
(2)解法一:当n=1时, ,∴
,∴
∴ ……………………7分
……………………7分
∵ ∴
∴ ………………8分
………………8分
∴


……

相加: +…+
+…+ ………………10分
………………10分
即: …+
…+ =
=
∴ ………………12分
………………12分
 ………14分
………14分
解法二:同解法一,得 …………………7分
…………………7分
∵ ∴
∴ ………………8分
………………8分
= =…=
=…= …+
…+
= …+
…+ ……………………10分
……………………10分
= ∴
∴  ……………12分
……………12分
 ………14分
………14分
 =1(n∈N*) ∴
=1(n∈N*) ∴ =1
=1两式相减:
 ∴
∴ ………………3分
………………3分∴{
 }是公比为
}是公比为 的等比数列 …………………6分
的等比数列 …………………6分(2)解法一:当n=1时,
 ,∴
,∴
∴
 ……………………7分
……………………7分∵
 ∴
∴ ………………8分
………………8分∴



……

相加:
 +…+
+…+ ………………10分
………………10分即:
 …+
…+ =
=
∴
 ………………12分
………………12分 ………14分
………14分解法二:同解法一,得
 …………………7分
…………………7分∵
 ∴
∴ ………………8分
………………8分=
 =…=
=…= …+
…+
=
 …+
…+ ……………………10分
……………………10分=
 ∴
∴  ……………12分
……………12分 ………14分
………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
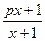 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;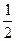 (cn+
(cn+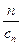 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;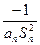 ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.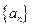 是等差数列,且
是等差数列,且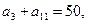 又
又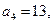 则
则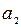 =" " ( )
=" " ( )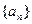 的前n项和
的前n项和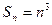 则
则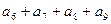 等于( )
等于( )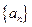 中,
中,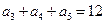 ,那么
,那么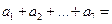 ( )
( )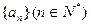 前12项,如下表所示:
前12项,如下表所示: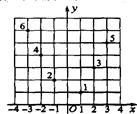
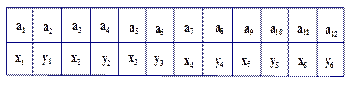
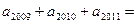
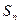 为等比数列
为等比数列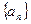 的前n项和,
的前n项和, ,则
,则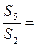 ( )
( )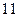

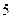
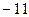
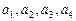 是等差数列,且满足
是等差数列,且满足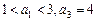 ,若
,若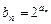 ,给出下列命题:
,给出下列命题: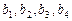 是一个等比数列; (2)
是一个等比数列; (2)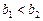 ; (3)
; (3)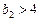 ; (4)
; (4)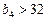 ; (5)
; (5)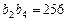 .
. ,
, ,对平面上任意一点
,对平面上任意一点 ,记
,记 为
为 的对称点,
的对称点, 为
为 的对称点,
的对称点, 为
为 为
为 为
为 关于
关于 为
为 为
为 …。则
…。则 =
=