题目内容
 的周长为
的周长为 ,且
,且 .
.(Ⅰ) 求边
 的长;
的长;(Ⅱ) 若
 的面积为
的面积为 ,求角
,求角 的度数.
的度数.(Ⅰ) ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
本题考查利用正弦定理、余弦定理解三角形。在解题中要注意定理得变形应用尤其是边角互化。
解:(Ⅰ)由题意及正弦定理,得 ,
,
 ,两式相减,得
,两式相减,得 .
.
(Ⅱ)由 的面积
的面积 ,得
,得 ,
,
由余弦定理,得
 ,
,
所以
解:(Ⅰ)由题意及正弦定理,得
 ,
, ,两式相减,得
,两式相减,得 .
. (Ⅱ)由
 的面积
的面积 ,得
,得 ,
,由余弦定理,得

 ,
,所以


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
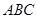 中,
中,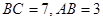 ,且
,且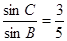 .
.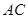 ; (Ⅱ)求
; (Ⅱ)求 .
. 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且满足
,且满足 ,
, .
.
 ,求边长
,求边长 中,若
中,若 ,
, ,
, ,则
,则


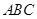 中,角
中,角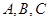 所对的边分别为
所对的边分别为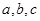 ,已知
,已知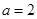 ,
,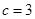 ,
,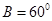 .
.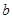 的值; (2)求
的值; (2)求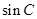 的值.
的值. 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, .
. 的值; 2) 求
的值; 2) 求 的值.
的值. 中, 已知
中, 已知 则
则
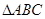 中,若
中,若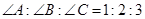 ,则
,则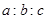 等于( )
等于( )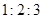
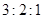
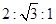
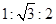
 中,若
中,若 ,则
,则