题目内容
【题目】方程 ![]() 在(0,2π)内有相异两解α,β,则α+β=
在(0,2π)内有相异两解α,β,则α+β=
【答案】![]() 或
或 ![]()
![]()
【解析】解:∵sinx+ ![]() cosx+a=0,
cosx+a=0,
∴﹣a=sinx+ ![]() cosx=2(
cosx=2( ![]() sinx+
sinx+ ![]() cosx)=2sin(x+
cosx)=2sin(x+ ![]() ),
),
令f(x)=2sin(x+ ![]() ),y=﹣a,
),y=﹣a,
∵0<x<2π,
∴ ![]() <x+
<x+ ![]() <2π+
<2π+ ![]() =
= ![]() ,
,
在同一坐标系中作出f(x)=2sin(x+ ![]() )与y=﹣a的图象,
)与y=﹣a的图象,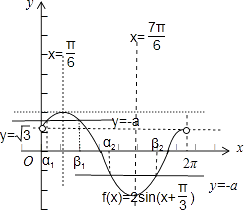
由图知,当x= ![]() ,即x+
,即x+ ![]() =
= ![]() 时,f(x)取到最大值2,当x=
时,f(x)取到最大值2,当x= ![]() 时,x+
时,x+ ![]() =
= ![]() +
+ ![]() =
= ![]() ,f(x)取到最小值﹣2;
,f(x)取到最小值﹣2;
方程sinx+ ![]() cosx+a=0在(0,2π)内有相异两解α,β直线y=﹣a与曲线f(x)=2sin(x+
cosx+a=0在(0,2π)内有相异两解α,β直线y=﹣a与曲线f(x)=2sin(x+ ![]() )在(0,2π)内有两个不同的交点,
)在(0,2π)内有两个不同的交点,
当交点的横坐标分别为α1与β1时,α1+β1= ![]() ;
;
当交点的横坐标分别为α2与β2时,α2+β2= ![]() ;
;
∴α+β= ![]() 或
或 ![]() .
.
所以答案是: ![]() 或
或 ![]() .
.
【考点精析】掌握两角和与差的正弦公式和函数的零点与方程根的关系是解答本题的根本,需要知道两角和与差的正弦公式:![]() ;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.
;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.

练习册系列答案
相关题目