题目内容
(1)已知α,β都为锐角,sinα=
,cos(α+β)=
,求sinβ与cosβ的值
(2)已知tanα=
,tanβ=-2,0°<α<90°,270°<β<360° 求α+β的值.
| 1 |
| 7 |
5
| ||
| 14 |
(2)已知tanα=
| 1 |
| 3 |
分析:(1)由α与β都为锐角,以及sinα与cos(α+β)的值,利用同角三角函数间的基本关系求出cosα与sin(α+β)的值,根据β=[(α+β)-α],利用两角和与差的正弦函数公式化简,将各自的值代入计算求出sinβ的值,再利用同角三角函数间的基本关系即可求出cosβ的值;
(2)根据tanα的值及α的范围,确定出α的具体范围,进而确定出α+β的范围,利用两角和与差的正切函数公式化简tan(α+β),将各自的值代入计算求出值,再利用特殊角的三角函数值即可确定出α+β的值.
(2)根据tanα的值及α的范围,确定出α的具体范围,进而确定出α+β的范围,利用两角和与差的正切函数公式化简tan(α+β),将各自的值代入计算求出值,再利用特殊角的三角函数值即可确定出α+β的值.
解答:解:(1)∵α,β都为锐角,sinα=
,cos(α+β)=
,
∴cosα=
=
,sin(α+β)=
=
,
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=
×
-
×
=
,
cosβ=
=
;
(2)∵tanα=
<1,tanβ=-2,0<α<45°,270°<β<360°,
∴270°<α+β<405°,
∴tan(α+β)=
=
=-1,
则α+β=315°.
| 1 |
| 7 |
5
| ||
| 14 |
∴cosα=
| 1-sin2α |
4
| ||
| 7 |
| 1-cos2(α+β) |
| 11 |
| 14 |
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=
| 11 |
| 14 |
4
| ||
| 7 |
5
| ||
| 14 |
| 1 |
| 7 |
39
| ||
| 98 |
cosβ=
| 1-sin2β |
| 71 |
| 98 |
(2)∵tanα=
| 1 |
| 3 |
∴270°<α+β<405°,
∴tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
| ||
1+
|
则α+β=315°.
点评:此题考查了两角和与差的余弦函数公式,同角三角函数间的基本关系,以及两角和与差的正切函数公式,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
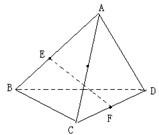 如图,在四面体ABCD中,已知所有棱长都为a,点E、F分别是AB、CD的中点.
如图,在四面体ABCD中,已知所有棱长都为a,点E、F分别是AB、CD的中点.