题目内容
 如图,已知PA⊥平面ABC,且
如图,已知PA⊥平面ABC,且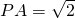 ,等腰直角三角形ABC中,AB=BC=1,AB⊥BC,AD⊥PB于D,AE⊥PC于E.
,等腰直角三角形ABC中,AB=BC=1,AB⊥BC,AD⊥PB于D,AE⊥PC于E.
(1)求证:PC⊥平面ADE;
(2)求点D到平面ABC的距离.
(1)证明:因为PA⊥平面ABC,所以PA⊥BC,
又AB⊥BC,且PA∩AB=A,所以BC⊥平面PAB,
因为AD?平面PAB,所以BC⊥AD.…(3分)
又AD⊥PB,BC∩PB=B,所以AD⊥平面PBC,
因为PC?平面PBC,所以PC⊥AD,
又PC⊥AE,AD∩AE=A,所以PC⊥平面ADE.…(6分)
(2)解:过D点作DF⊥BA垂直为E,

由题意知DF⊥面ABC,即DF为所求距离.…(8分)
由题设得DF∥PA,所以△BDE∽△BAP,即DF= ,
,
又∵△BDA∽△BAP,∴
即BD= ,∴
,∴ .
.
∴DF= .…(11分)
.…(11分)
即点D到平面ABC的距离为 .…(12分)
.…(12分)
分析:(1)利用线面垂直的性质与判定,证明PC⊥平面ADE,证出PC⊥AD,PC⊥AE即可;
(2)过D点作DF⊥BA垂直为E,由题意知DF⊥面ABC,即DF为所求距离,利用三角形的相似,可得结论.
点评:本题考查线面垂直的性质与判定,考查点到面的距离,掌握线面垂直的性质与判定,作出点到面的距离的线段是关键.
又AB⊥BC,且PA∩AB=A,所以BC⊥平面PAB,
因为AD?平面PAB,所以BC⊥AD.…(3分)
又AD⊥PB,BC∩PB=B,所以AD⊥平面PBC,
因为PC?平面PBC,所以PC⊥AD,
又PC⊥AE,AD∩AE=A,所以PC⊥平面ADE.…(6分)
(2)解:过D点作DF⊥BA垂直为E,

由题意知DF⊥面ABC,即DF为所求距离.…(8分)
由题设得DF∥PA,所以△BDE∽△BAP,即DF=
 ,
,又∵△BDA∽△BAP,∴

即BD=
 ,∴
,∴ .
.∴DF=
 .…(11分)
.…(11分)即点D到平面ABC的距离为
 .…(12分)
.…(12分)分析:(1)利用线面垂直的性质与判定,证明PC⊥平面ADE,证出PC⊥AD,PC⊥AE即可;
(2)过D点作DF⊥BA垂直为E,由题意知DF⊥面ABC,即DF为所求距离,利用三角形的相似,可得结论.
点评:本题考查线面垂直的性质与判定,考查点到面的距离,掌握线面垂直的性质与判定,作出点到面的距离的线段是关键.

练习册系列答案
相关题目
 (2012•丹东模拟)如图,已知PA⊥平面ABCD,ABCD是矩形,PA=AB=1,
(2012•丹东模拟)如图,已知PA⊥平面ABCD,ABCD是矩形,PA=AB=1, (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且 (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点. (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.