题目内容
已知函数![]() (
(![]() ∈R且都为常数)的导函数
∈R且都为常数)的导函数![]() ,且
,且![]() =7,设F
=7,设F![]() R);
R);
(1)当![]() <2时,求F(
<2时,求F(![]() )的极小值;
)的极小值;
(2)若对任意的![]() ∈[0,+∞),都有F(
∈[0,+∞),都有F(![]() )≥0成立,求
)≥0成立,求![]() 的取值范围并证明
的取值范围并证明
![]() .
.
解:(1)∵![]() ∴
∴![]() =2,
=2,![]() .
.
∴![]() . 又∵
. 又∵![]() , ∴
, ∴![]() 4,
4,
∴![]()
∵F![]() .
.
∴当![]() =0时,F(
=0时,F(![]() )取得极小值4.
)取得极小值4.
(2)由(1)知F(![]() )=
)=![]() .
.
∴F(![]() )≥0在[0,+∞)恒成立
)≥0在[0,+∞)恒成立![]() 当
当![]() [0,+∞)时,F
[0,+∞)时,F![]() ≥0.
≥0.
①若![]() ,即
,即![]() <2时,由(1)可知F
<2时,由(1)可知F![]() =F(0)=4>0,符合题意;
=F(0)=4>0,符合题意;
②若![]() ≤0,即
≤0,即![]() ≥2时,由
≥2时,由![]() 求得
求得![]() ,且
,且![]()
∴当![]() ∈[0,+∞)时,F
∈[0,+∞)时,F![]() =F(
=F(![]() )≥0,
)≥0,
即![]() ≥0,解不等式得2≤
≥0,解不等式得2≤![]() ≤5.
≤5.
综上所述,应有![]() ≤5.要证不等式
≤5.要证不等式![]() ,
,
只需证![]() ,∵
,∵![]() ≤5,
≤5,
∴![]() ≥2,
≥2,![]() ≤2(当
≤2(当![]() 5时,等号成立).
5时,等号成立).

练习册系列答案
相关题目
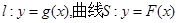 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有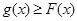 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.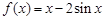 .求证:
.求证: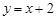 为曲线
为曲线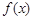 的“上夹线”.
的“上夹线”.
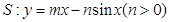 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明. . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”. .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.


 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.