题目内容
【题目】已知圆![]() ,点
,点![]() 是直线
是直线![]() 上的一动点,过点
上的一动点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
(1)当切线![]() 的长度为
的长度为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)若![]() 的外接圆为圆
的外接圆为圆![]() ,试问:当
,试问:当![]() 在直线
在直线![]() 上运动时,圆
上运动时,圆![]() 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段![]() 长度的最小值.
长度的最小值.
【答案】(1)![]() 或
或![]() (2)圆过定点
(2)圆过定点![]() (3)
(3)![]()
【解析】
试题分析:(1)根据圆M的标准方程即可求出半径r=2和圆心M坐标(0,4),并可设P(2b,b),从而由条件便可求出|MP|=![]() =4,这样便可求出b的值,即得出点P的坐标;(2)容易求出圆N的圆心坐标(b,
=4,这样便可求出b的值,即得出点P的坐标;(2)容易求出圆N的圆心坐标(b,![]() ),及半径,从而可得出圆N的标准方程,化简后可得到(2x+y-4)b-(x2+y2-4y)=0,从而可建立关于x,y的方程,解出x,y,便可得出圆N所过的定点坐标;(3)可写出圆N和圆M的一般方程,联立这两个一般方程即可求出相交弦AB的直线方程,进而求出圆心M到直线AB的距离,从而求出弦长
),及半径,从而可得出圆N的标准方程,化简后可得到(2x+y-4)b-(x2+y2-4y)=0,从而可建立关于x,y的方程,解出x,y,便可得出圆N所过的定点坐标;(3)可写出圆N和圆M的一般方程,联立这两个一般方程即可求出相交弦AB的直线方程,进而求出圆心M到直线AB的距离,从而求出弦长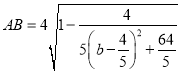 ,显然可看出
,显然可看出![]() 时,AB取最小值,并求出该最小值
时,AB取最小值,并求出该最小值
试题解析:(1)由题意知,圆![]() 的半径
的半径![]() ,设
,设![]() ,
,
∵![]() 是圆
是圆![]() 的一条切线,∴
的一条切线,∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() 或
或![]() . ………………………4分
. ………………………4分
(2)设![]() ,∵
,∵![]() ,
,
∴经过![]() 三点的圆
三点的圆![]() 以
以![]() 为直径,
为直径,
其方程为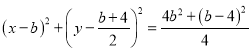 , ……………………6分
, ……………………6分
即![]() ,
,
由![]() , ………………………8分
, ………………………8分
解得![]() 或
或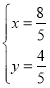 ,
,
∴圆过定点![]() , ………………………10分
, ………………………10分
(3)因为圆![]() 方程为
方程为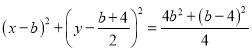 ,
,
即![]() ,
,
圆![]() ,即
,即![]() ,
,
②-①得:圆![]() 方程与圆
方程与圆![]() 相交弦
相交弦![]() 所在直线方程为:
所在直线方程为:
![]() , ………………………12分
, ………………………12分
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
 ,…………14分
,…………14分
当![]() 时,
时,![]() 有最小值
有最小值![]() . ………………………16分
. ………………………16分

练习册系列答案
相关题目