题目内容
7.已知函数f(x)满足f(3x)=x,则f(2)=( )| A. | log32 | B. | log23 | C. | ln2 | D. | ln3 |
分析 设3x=t,则x=log3t,从而f(t)=log3t,由此能求出f(2).
解答 解:∵函数f(x)满足f(3x)=x,
设3x=t,则x=log3t,
∴f(t)=log3t,
∴f(2)=log32.
故选:A.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意换元法的合理运用.

练习册系列答案
相关题目
12.己知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则$\frac{2{S}_{n}+144}{{a}_{n}+5}$的最小值为( )
| A. | 4$\sqrt{19}$-4 | B. | $\frac{27}{2}$ | C. | $\frac{121}{9}$ | D. | $\frac{67}{5}$ |
19.已知命题p:?x∈R,2x=5,则¬p为( )
| A. | ?x∉R,2x≠5 | B. | ?x∈R,2x≠5 | C. | ?x∉R,2x≠5 | D. | ?x∈R,2x≠5 |
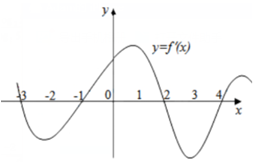 如图是y=f(x)的导函数的图象,现有四种说法:
如图是y=f(x)的导函数的图象,现有四种说法: