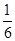题目内容
连续抛掷一枚骰子两次,得到的点数依次记为m、n,则点(m,n)恰能落在不等式组
所表示的区域内的概率为______.
|
根据题意,m、n的都有6种情况,则点(m,n)的情况有6×6=36种;
解不等式组
可得:0<x+y<6,且x≤3,
点(m,n)位于其表示的区域内的有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2)共9种;
则点(m,n)位于其表示的区域内的概率为
=
;
故答案为
.
解不等式组
|
点(m,n)位于其表示的区域内的有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2)共9种;
则点(m,n)位于其表示的区域内的概率为
| 9 |
| 36 |
| 1 |
| 4 |
故答案为
| 1 |
| 4 |

练习册系列答案
相关题目
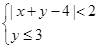 所表示的平面区域内的概率为( )
所表示的平面区域内的概率为( )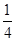 B.
B. C.
C. D.
D.