题目内容
 将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且a1=a13=1,a31=
将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且a1=a13=1,a31=| 5 | 3 |
(1)求数列{cn},{sn}的通项公式.
(2)求数列{cn}的前n项和Tn的表达式.
分析:(1)利用表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},可得bn=dn-d+1,前n行共有1+2+3+…+n=
个数,再结合a1=a13=1,a31=
,可求数列{bn},{cn},{sn}的通项公式;
(2)根据数列{cn}的通项特点,利用错位相减法,可求数列{cn}的前n项和Tn的表达式.
| n(n+1) |
| 2 |
| 5 |
| 3 |
(2)根据数列{cn}的通项特点,利用错位相减法,可求数列{cn}的前n项和Tn的表达式.
解答:解:(1)∵表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},
∴bn=dn-d+1,前n行共有1+2+3+…+n=
个数,
因为13=
+3,所以a13=b5×q2,即(4d+1)q2=1
又因为31=
+3,所以a31=b8×q2,即(7d+1)q2=
,
解得:d=2,q=
,…(4分)
所以:bn=2n-1,
∵各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},
∴cn=bn(
)n-1=
,
∵第n行所有数的和为sn,
∴Sn=
=
(2n-1)•
.…(7分)
(2)∵cn=bn(
)n-1=
,
∴Tn=
+
+
+…+
,…①…(8分)
Tn=
+
+
+…+
…②…(9分)
①②两式相减得:
Tn=1+2(
+
+…+
)-
=1+2×
-
=2-
…(13分)
所以:Tn=3-
.…(14分)
∴bn=dn-d+1,前n行共有1+2+3+…+n=
| n(n+1) |
| 2 |
因为13=
| 4×5 |
| 2 |
又因为31=
| 7×8 |
| 2 |
| 5 |
| 3 |
解得:d=2,q=
| 1 |
| 3 |
所以:bn=2n-1,
∵各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},
∴cn=bn(
| 1 |
| 3 |
| 2n-1 |
| 3n-1 |
∵第n行所有数的和为sn,
∴Sn=
(2n-1)(1-
| ||
1-
|
| 3 |
| 2 |
| 3n-1 |
| 3n |
(2)∵cn=bn(
| 1 |
| 3 |
| 2n-1 |
| 3n-1 |
∴Tn=
| 1 |
| 1 |
| 3 |
| 3 |
| 5 |
| 32 |
| 2n-1 |
| 3n-1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 32 |
| 5 |
| 33 |
| 2n-1 |
| 3n |
①②两式相减得:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n-1 |
| 2n-1 |
| 3n |
=1+2×
| ||||
1-
|
| 2n-1 |
| 3n |
| 2n+2 |
| 3n |
所以:Tn=3-
| n+1 |
| 3n-1 |
点评:本题考查数阵与数列的额连续,考查数列的通项与求和,考查错位相减法的运用,针对数列通项的特点,选择正确的方法是关键.

练习册系列答案
相关题目
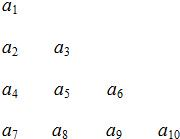 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:a1a2a3a4a5a6a7a8a9a10…记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:a1a2a3a4a5a6a7a8a9a10…记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足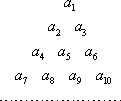
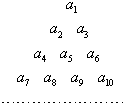 将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且
将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且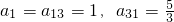 .
. .
.