题目内容
已知直线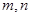 与平面
与平面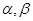 ,给出下列三个结论:①若
,给出下列三个结论:①若 ∥
∥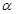 ,
,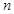 ∥
∥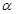 ,则
,则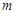 ∥
∥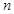 ;
;
②若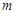 ∥
∥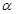 ,
,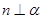 ,则
,则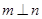 ; ③若
; ③若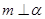 ,
,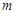 ∥
∥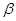 ,则
,则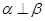 .
.
其中正确的个数是 ( )
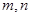 与平面
与平面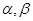 ,给出下列三个结论:①若
,给出下列三个结论:①若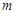 ∥
∥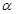 ,
,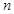 ∥
∥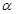 ,则
,则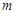 ∥
∥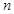 ;
;②若
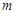 ∥
∥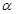 ,
,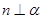 ,则
,则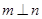 ; ③若
; ③若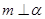 ,
,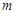 ∥
∥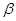 ,则
,则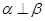 .
.其中正确的个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
C
试题分析:若
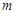 ∥
∥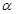 ,
,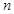 ∥
∥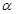 ,则
,则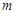 ∥
∥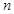 或
或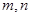 相交或
相交或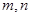 是异面直线,故①不正确;根据线面平行的性质定理,
是异面直线,故①不正确;根据线面平行的性质定理,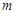 ∥
∥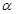 时,在面
时,在面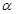 内必存在一条直线
内必存在一条直线 与
与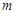 平行,即
平行,即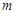 ∥
∥ 。因为
。因为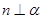 ,则
,则 ,所以
,所以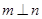 ,故②正确;根据线面平行的性质定理,
,故②正确;根据线面平行的性质定理,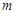 ∥
∥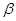 时,在面
时,在面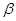 内必存在一条直线
内必存在一条直线 与
与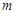 平行,即
平行,即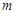 ∥
∥ ,因为
,因为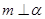 ,所以
,所以 ,因为
,因为 ,所以
,所以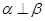 故③正确。综上可得正确的个数是2个,故C正确。
故③正确。综上可得正确的个数是2个,故C正确。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
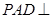 底面
底面 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形, ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.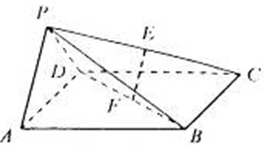
 平面
平面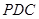 .
.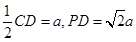 .
.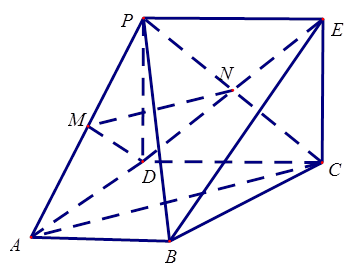
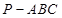 中,平面
中,平面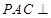 平面
平面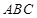 ,
,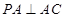 ,
,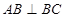 .设
.设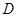 ,
,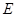 分别为
分别为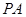 ,
,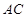 中点.
中点.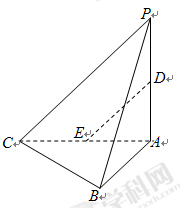
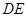 ∥平面
∥平面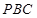 ;
;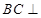 平面
平面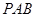 ;
;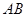 上是否存在点
上是否存在点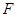 ,使得过三点
,使得过三点 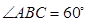 ,
,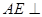 平面ABCD,
平面ABCD,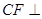 平面ABCD,
平面ABCD,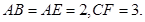
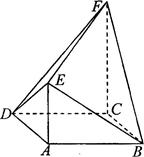
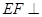 平面BDE;
平面BDE;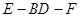 的大小.
的大小.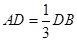 ,点C为圆O上一点,且
,点C为圆O上一点,且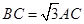 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.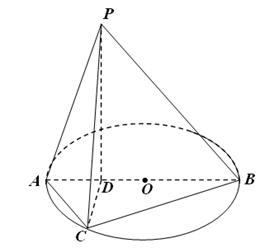
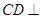 平面
平面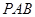 ;
;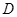 到平面
到平面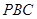 的距离.
的距离.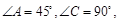
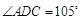 ,
,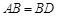 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD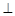 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

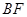 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值. 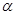 、
、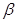 是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误的是
是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误的是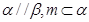 ,则
,则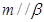
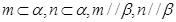 ,则
,则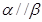
 ,则
,则
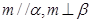 ,则
,则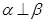
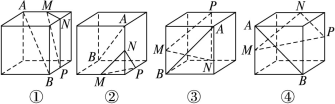
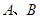 为正方体的两个顶点,
为正方体的两个顶点,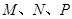 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出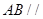 平面
平面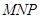 的图形的序号是( )
的图形的序号是( )