题目内容
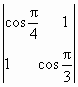
(1)将形如
的符号称二阶行列式,现规定
=a11a22-a12a21.
试计算二阶行列式
的值;
(2)已知tan(
+a)=-
,求
.
|
|
试计算二阶行列式
|
(2)已知tan(
| π |
| 4 |
| 1 |
| 2 |
| sin2a-2cos2a |
| 1+tana |
分析:(1)由于
=a11a22-a12a21,根据这个规定可以所求二阶行列式的结果.
(2)把所求式子的分子第一项利用二倍角的正弦函数公式化简,分母第二项利用二倍角的余弦函数公式化简,然后利用同角三角函数间的基本关系化简,将求出的tanα的值代入即可求出值.
|
(2)把所求式子的分子第一项利用二倍角的正弦函数公式化简,分母第二项利用二倍角的余弦函数公式化简,然后利用同角三角函数间的基本关系化简,将求出的tanα的值代入即可求出值.
解答:解:(1)
=cos
cos
-1=
-1;
(2)∵tan(
+a)=-
,∴
=-
,
整理得:2+2tanα=-1+tanα,
解得:tanα=-3;…(4分)
=
=
=
=
=
.…(8分)
故答案为:
.
|
| π |
| 4 |
| π |
| 3 |
| ||
| 4 |
(2)∵tan(
| π |
| 4 |
| 1 |
| 2 |
| 1+tanα |
| 1-tanα |
| 1 |
| 2 |
整理得:2+2tanα=-1+tanα,
解得:tanα=-3;…(4分)
| sin2a-2cos2a |
| 1+tana |
| 2sinαcosα-2cos2α |
| 1+tanα |
| 2sinαcosα-2cos2α |
| (1+tanα)(sin2α+cos2α) |
| 2tanα-2 |
| (1+tanα)(tan2α+1) |
| -6-2 |
| -2×10 |
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题考查了二阶矩阵、三角函数的恒等变换及化简求值,考查了两角和与差的正切函数公式,二倍角的正弦、余弦函数公式,同角三角函数间的基本关系,以及特殊角的三角函数值,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
相关题目
 的值;
的值; 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 的值;(5分)
的值;(5分) 。(5分)
。(5分) 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 =a11a22-a12a21.
=a11a22-a12a21.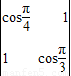 的值;
的值;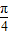 +a)=-
+a)=- ,求
,求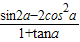 .
.