题目内容
“根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.”某市交警在该市一交通岗前设点对过往的车辆进行抽查,经过一晚的抽查,共查出酒后驾车者60名,图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图.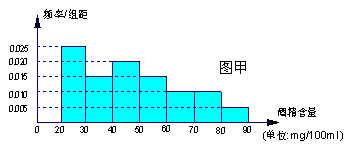
(1)统计方法中,同一组数据常用该组区间的中点值作为代表,图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计,求出图乙输出的S的值,并说明S的统计意义;(图乙中数据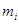 与
与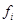 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率) 
(2)本次行动中,吴、李两位先生都被酒精测试仪测得酒精浓度属于70~90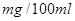 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90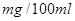 范围的酒后驾车者中随机抽出2人抽血检验,设
范围的酒后驾车者中随机抽出2人抽血检验,设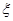 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求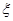 的分布列,并求吴、李两位先生至少有1人被抽中的概率;
的分布列,并求吴、李两位先生至少有1人被抽中的概率;
详见解析
解析试题分析:(1)由图乙知输出的 7,代入已知数据可求, S的统计意义为60名酒后驾车者血液的酒精浓度的平均值.
7,代入已知数据可求, S的统计意义为60名酒后驾车者血液的酒精浓度的平均值.
(2)根据直方图可求酒精浓度属于70-90mg/100ml的范围的人数,然后求出 ξ取值, ,根据超几何分布进而求出相应的概率,即可求解分布列,吴、李两位先生至少有1人被抽中的概率
,根据超几何分布进而求出相应的概率,即可求解分布列,吴、李两位先生至少有1人被抽中的概率 .
.
试题解析:解:(1)由图乙知输出的
=
=47(mg/100ml) 5分
S的统计意义为60名酒后驾车者血液的酒精浓度的平均值. 6分
(2)酒精浓度属于70~90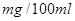 的范围的人数为
的范围的人数为 7分
7分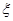 的可能取值为0,1,2
的可能取值为0,1,2 ,
, ,
, 8分
8分
分布列如下: 9分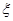
0 1 2 P 


吴、李两位先生至少有1人被抽中的概率
 .
.
(或 ) 12分
) 12分
考点:1.程序框图的意义;2.离散型随机变量的分布列.

(本小题满分12分)一工厂生产甲、乙、丙三种样式的杯子,每种样式均有 和
和 两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取
两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取 个,其中有甲样式杯子
个,其中有甲样式杯子 个.
个.
| 型号 | 甲样式 | 乙样式 | 丙样式 |
 |  |  |  |
 |  |  |  |
(1)求
 的值;
的值; (2)用分层抽样的方法在甲样式杯子中抽取一个容量为
 的样本,从这个样本中任取
的样本,从这个样本中任取 个杯子,求至少有
个杯子,求至少有 个
个 杯子的概率.
杯子的概率. 某城市随机抽取一个月( 天)的空气质量指数
天)的空气质量指数 监测数据,统计结果如下:
监测数据,统计结果如下:
 |  |  |  |  |  |  |  |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 |  |  |  |  |  |  |  |
(1)根据以上数据估计该城市这
 天空气质量指数
天空气质量指数 的平均值;
的平均值;(2)若该城市某企业因空气污染每天造成的经济损失
 (单位:元)与空气质量指数
(单位:元)与空气质量指数 (记为
(记为 )的
)的关系式为

若在本月
 天中随机抽取一天,试估计该天经济损失
天中随机抽取一天,试估计该天经济损失 大于
大于 元且不超过
元且不超过 元的概率.
元的概率. 某中学将 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班 人,吴老师采用
人,吴老师采用 、
、 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下:
记成绩不低于 分者为“成绩优秀”.
分者为“成绩优秀”.
(1)在乙班样本的 个个体中,从不低于
个个体中,从不低于 分的成绩中随机抽取
分的成绩中随机抽取 个,记随机变量
个,记随机变量 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;
(2)由以上统计数据填写下面 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
| | 甲班( 方式) 方式) | 乙班( 方式) 方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
附:
| P(K2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |
χ2=

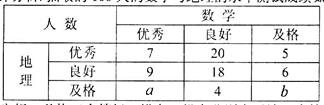
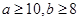 ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
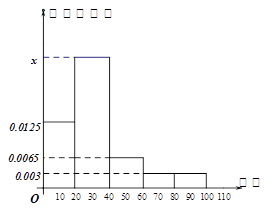
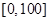 ,样本数据分组为
,样本数据分组为 ,
,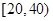 ,
,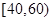 ,
,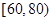 ,
,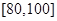 .
.
 的值;
的值;