题目内容
(本小题满分12分)一工厂生产甲、乙、丙三种样式的杯子,每种样式均有 和
和 两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取
两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取 个,其中有甲样式杯子
个,其中有甲样式杯子 个.
个.
| 型号 | 甲样式 | 乙样式 | 丙样式 |
 |  |  |  |
 |  |  |  |
(1)求
 的值;
的值; (2)用分层抽样的方法在甲样式杯子中抽取一个容量为
 的样本,从这个样本中任取
的样本,从这个样本中任取 个杯子,求至少有
个杯子,求至少有 个
个 杯子的概率.
杯子的概率.
(1)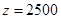 ;(2)
;(2)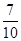 .
.
解析试题分析:(1)先求出在丙、乙样式的杯子中所抽取的杯子数目,然后利用分层抽样中每层的入样比相等得到乙样式的杯子的总数,从而求出 的值;(2)先确定所抽取的样本中
的值;(2)先确定所抽取的样本中 和
和 杯子各自的数目,并进行编号,利用列举法求出基本事件的总数与问题中涉及的事件所包含的基本事件,利用古典概型的概率计算公式求出相应事件的概率.
杯子各自的数目,并进行编号,利用列举法求出基本事件的总数与问题中涉及的事件所包含的基本事件,利用古典概型的概率计算公式求出相应事件的概率.
(1)设该厂本月生产的乙样式的杯子为 个,在丙样式的杯子中抽取
个,在丙样式的杯子中抽取 个,
个,
由题意得,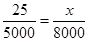 ,所以
,所以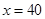 ,
,
则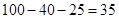 ,所以,
,所以,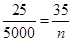 ,
,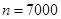 ,故
,故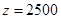 ;
;
(2)设所抽取样本中有 个
个 的杯子,
的杯子,
因为分层抽样的方法中在甲样式杯子中抽取一个容量为 的样本,所以
的样本,所以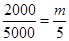 ,解得
,解得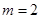 ,
,
也就是抽取了 个
个 杯子,
杯子, 个
个 杯子,
杯子,
分别记作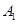 、
、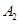 、
、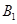 、
、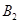 、
、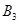 ,则从中任取
,则从中任取 个的所有的基本事件为:
个的所有的基本事件为: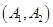 、
、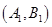 、
、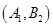 、
、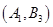 、
、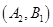 、
、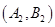 、
、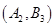 、
、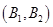 、
、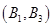 、
、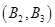 ,
,
共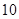 个,其中至少有
个,其中至少有 个
个 的杯子的基本事件:
的杯子的基本事件: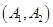 、
、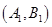 、
、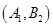 、
、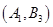 、
、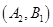 、
、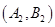 、
、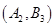 ,
,
所以从中任取 个,至少有
个,至少有 个
个 杯子的概率为
杯子的概率为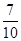 .
.
考点:1.分层抽样;2.古典概型

某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: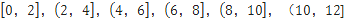 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.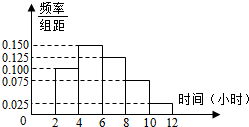
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有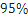 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2=
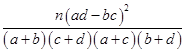
从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有一个的概率.
(12分)(2011•福建)某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X | 1 | 2 | 3 | 4 | 5 |
| f | a | 0.2 | 0.45 | b | c |
(Ⅱ)在(Ⅰ)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2,这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
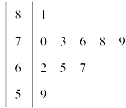

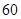 名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过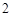 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过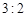 .
.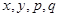 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).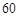 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定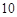 人,若需从这
人,若需从这 人进行问卷调查,设
人进行问卷调查,设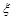 为选取的
为选取的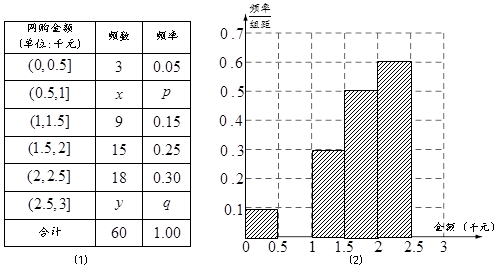
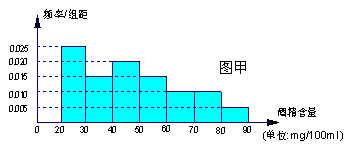
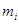 与
与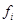 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率) 
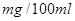 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90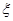 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求