题目内容
已知椭圆3x2+y2=12,过原点且倾斜角分别为θ和π-θ(0<θ≤
答案: 12 ![]() 由对称性,知四边形ABCD为矩形.
由对称性,知四边形ABCD为矩形.
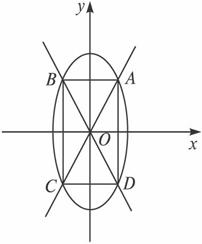
设AC的方程为y=kx,∵θ∈(0,![]() ],∴0<k≤1.与3x2+y2=12联立得3x2+k2x2=12,x2=
],∴0<k≤1.与3x2+y2=12联立得3x2+k2x2=12,x2=![]() ,y2=
,y2=![]() ,x2y2=
,x2y2=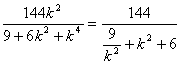 .
.
∵t=k2+![]() 在k2∈(0,3)时为减函数,k2∈(3,+∞)时为增函数,又∵0<k≤1,
在k2∈(0,3)时为减函数,k2∈(3,+∞)时为增函数,又∵0<k≤1,
∴k2=1时,t取最小值10.∴x2y2≥![]() ,|xy|≥
,|xy|≥![]() .
.
∴S四边形ABCD的最大值为4|xy|=12,此时θ=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目