题目内容
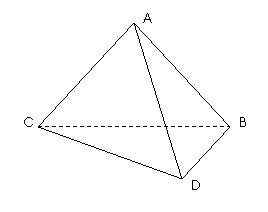
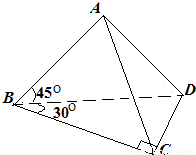
已知如图,平面ABD⊥平面BCD,∠BAD=∠BCD=90°,∠ABD=45°,∠CBD=30°.(Ⅰ)异面直线AB、CD所成的角为α,异面直线AC、BD所成的角为β,求证:α=β;
(Ⅱ)求二面角B-AC-D的余弦值的绝对值.
【答案】分析:(Ⅰ)证明AO⊥面BCD,建立空间直角坐标系,确定向量的坐标,利用向量的夹角公式,即可求得结论;
(Ⅱ)求出平面ABC、平面ACD一个法向量,利用向量的夹角公式,即可求二面角B-AC-D的余弦值的绝对值.
解答: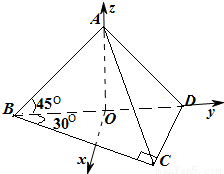 (Ⅰ)证明:设BD的中点为O,∠BAD=90°,∠ABD=45°,∴∠BDA=45°,即AB=AD,∴AO⊥BD.
(Ⅰ)证明:设BD的中点为O,∠BAD=90°,∠ABD=45°,∴∠BDA=45°,即AB=AD,∴AO⊥BD.
∵平面ABD⊥平面BCD,∴AO⊥面BCD.
以过O点垂直于BD的直线为x轴,以直线BD为y轴,以直线OA为z,建立如图所示的空间直角坐标系A-xyz,设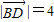 .
.
∴ ,
,
∴ ,
,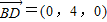 ,
,
∴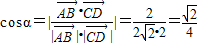 ,
,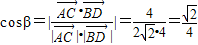 .
.
∵0°<α,β≤90°,∴α=β.…6分
(Ⅱ)解:设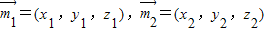 分别是平面ABC、平面ACD一个法向量,
分别是平面ABC、平面ACD一个法向量,
∴ ,即
,即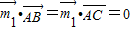 ,
,
∴ ,不妨取
,不妨取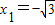 ,得
,得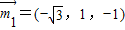 .
.
同理可求得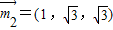 ,
,
∴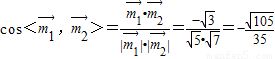 ,
,
所以二面角B-AC-D的余弦值的绝对值为 .…12分.
.…12分.
点评:本题考查空间角,考查向量知识的运用,确定平面的法向量,正确利用公式是关键.
(Ⅱ)求出平面ABC、平面ACD一个法向量,利用向量的夹角公式,即可求二面角B-AC-D的余弦值的绝对值.
解答:
 (Ⅰ)证明:设BD的中点为O,∠BAD=90°,∠ABD=45°,∴∠BDA=45°,即AB=AD,∴AO⊥BD.
(Ⅰ)证明:设BD的中点为O,∠BAD=90°,∠ABD=45°,∴∠BDA=45°,即AB=AD,∴AO⊥BD.∵平面ABD⊥平面BCD,∴AO⊥面BCD.
以过O点垂直于BD的直线为x轴,以直线BD为y轴,以直线OA为z,建立如图所示的空间直角坐标系A-xyz,设
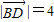 .
.∴
 ,
,∴
 ,
,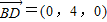 ,
,∴
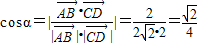 ,
,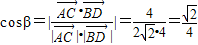 .
.∵0°<α,β≤90°,∴α=β.…6分
(Ⅱ)解:设
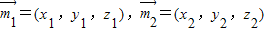 分别是平面ABC、平面ACD一个法向量,
分别是平面ABC、平面ACD一个法向量,∴
 ,即
,即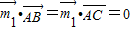 ,
,∴
 ,不妨取
,不妨取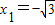 ,得
,得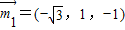 .
.同理可求得
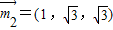 ,
,∴
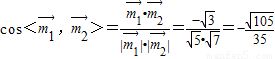 ,
,所以二面角B-AC-D的余弦值的绝对值为
 .…12分.
.…12分.点评:本题考查空间角,考查向量知识的运用,确定平面的法向量,正确利用公式是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
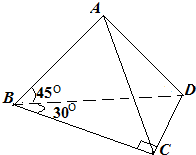 已知如图,平面ABD⊥平面BCD,∠BAD=∠BCD=90°,∠ABD=45°,∠CBD=30°.
已知如图,平面ABD⊥平面BCD,∠BAD=∠BCD=90°,∠ABD=45°,∠CBD=30°.